ЗАОЧНЫЙ КОНКУРС ПО МАТЕМАТИКЕ И ИНФОРМАТИКЕ

Весна 2000 г. Решения задач

Всюду в тексте буква "x" между двумя числами означает умножение.

1. Что больше: 102102102x103103 или 103103103x102102 ?
Решение. Эти числа равны: 102102102 x 103103 = (102 x 1001001) x (103 x 1001) = (103 x 1001001) x (102 x 1001) = 103103103 x 102102.

2. Сумма цифр числа x равна y, а сумма цифр числа y равна z. Может ли сумма x+y+z равняться 156 ?
Решение. Да. Например, x=139, y=13, z=4.

3. Можно ли написать на гранях кубика числа 1,2,3,4,5,6 (каждое число встречается один раз) так, чтобы числа на соседних гранях отличались не более чем на 2 ?
Решение. Нет. Либо 1 и 6, либо 1 и 5 будут на соседних гранях - а разность в любом из двух случаев больше 2.

4. Поднимаясь к себе в квартиру, Вася обычно отдыхает на полпути - на пятом этаже, проходя до и после отдыха одинаковое число ступенек. На каком этаже он живёт? (Первый этаж находится на уровне земли.)
Решение. На девятом: и до, и после отдыха он поднимается на 4 этажа.

5. Из любых 7 целых чисел можно выбрать два, разность квадратов которых делится на 11. Почему ?
Решение. Если два числа из 7 дают одинаковые остатки при делении на 11, то и их квадраты дают одинаковые остатки, поэтому разность квадратов делится на 11. Предположим, что все остатки различны. Разобьём все возможные остатки от деления на 11 на пары: (1,10), (2,9), (3,8), (4,7), (5,6) (остаток 0 останется без пары). Среди 7 наших остатков заведомо встретятся два, стоящих в одной паре (иначе их было бы не более шести: по одному из каждой пары да ещё ноль). Поэтому среди чисел есть два, сумма которых делится на 11. Осталось заметить, что разность квадратов чисел делится на их сумму.

6. Можно ли написать число из одних четвёрок (444...444), которое бы делилось на 8? (Приведите пример или объясните, почему такого числа нет.)
Решение. Нет, нельзя. 444...444/4=111...111 - нечётное число. А если бы 444...444 делилось на 8, частное от деления на 4 было бы чётным.

7. На встрече собрались все участники двух походов (некоторые были в обоих походах, некоторые - только в одном). В первом походе было две трети мальчиков и треть девочек, во втором - поровну тех и других. Какова минимальная и какова максимальная возможная доля мальчиков среди участников встречи?
Решение. Ответ: минимальная доля 2/5, максимальная 3/4. Действительно, на встрече М мальчиков, то в первом походе девочек было не более (1/2)М, а во втором - не более М (даже если все мальчики был в обоих походах). Поэтому всего девочек на встрече не более (1/2)М+М=(3/2)М. Значит, доля мальчиков не меньше 2/5. Если теперь обозначить за Д число девочек на встрече, то мальчиков не более Д+2Д=3Д (не более 2Д в первом походе и не более Д во втором). Поэтому доля мальчиков не больше 3/4.

8. В строчку написано несколько минусов. Два игрока по очереди переправляют один или два соседних минуса на плюс; выигрывает переправивший последний минус. Кто выигрывает при правильной игре: начинающий или его партнёр?
Решение. Выигрывает начинающий (при любом количестве минусов). Первым ходом он делит строчку пополам (если число минусов нечётно, переправляет средний минус, если чётно - два средних), а дальше ходит симметрично второму.

9. Представьте число 50 в виде суммы нескольких целых положительных чисел так, чтобы их произведение было как можно больше. Докажите, что ваш вариант - наилучший.
Решение. Ответ: 50=2+3+3+...+3 (16 троек). Покажем, что любой другой вариант можно улучшить. Если среди слагаемых есть число k>3, то, написав вместо него (k-2)+2, мы увеличим произведение. Поэтому все слагаемые должны быть не больше 3. Если среди слагаемых есть единицы, то вместо них можно написать их сумму (k вместо 1+1+...+1 (k единиц)) или, если единица всего одна, добавить её к какому-то слагаемому ((k+1) вместо k+1) - в обоих случаях произведение только увеличится. Осталось разобрать случай, когда среди слагаемых есть только двойки и тройки. Если двоек больше 2, то можно заменить три двойки на две тройки, увеличив произведение (3x3>2x2x2). Поэтому двоек должно быть не более 2, а остальные - тройки. Получается как раз то разбиение, которое указано в ответе.

10. Верно ли, что из любых 100 целых чисел можно выбрать два числа, разность которых делится на 37?
Решение. Да. Среди 100 чисел есть два, дающие одинаковые остатки при делении на 37 (так как различных остатков всего 37) - значит, их разность делится на 37.

11. Верно ли, что из любых 100 целых чисел можно выбрать два числа, сумма которых делится на 37?
Решение. Нет. Например, рассмотрим числа 1, 37+1, 37x2+1,...,37x99+1. Каждое из них даёт при делении на 37 остаток 1, поэтому сумма любых двух даёт остаток 2 (и, следовательно, не делится на 37).

12. Верно ли, что из любых 100 целых чисел можно выбрать несколько так, чтобы сумма выбранных чисел делилась на 37? (Число выбранных может быть любым от 1 до 100.)
Решение. Да. Обозначим наши числа a(1),...,a(100) и рассмотрим сто сумм a(1), a(1)+a(2), a(1)+a(2)+a(3),..., a(1)+a(2)+a(3)+...+a(100). Среди этих ста сумм есть две, дающие одинаковые остатки при делении на 37. Вычтя из суммы с большим количеством слагаемых сумму с меньшим количеством, мы получим сумму вида a(i+1)+a(i+2)+...+a(j) (здесь в первой сумме j слагаемых, во второй i, i меньше j), которая делится на 37.

13. Может ли целое положительное число после возведения в квадрат начинаться с десяти девяток?
Решение. Да. Например, 99999999999 (11 девяток) в квадрате равно 9999999999800000000001 (10 девяток и 10 нулей).

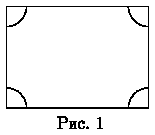
14. Кузов грузовика имеет форму прямоугольника 5 на 7 метров. В нём лежит трёхметровое бревно, в которое вбит гвоздь на расстоянии 1м от одного из концов. Грузовик трясётся, и бревно перекатывается по кузову и царапает пол. Нарисуйте, какая часть пола останется заведомо не поцарапанной.
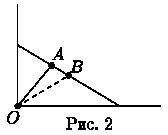
Решение. Ответ показан на рисунке 1 (радиусы кругов равны 1м). В решении есть тонкий момент (который не заметил почти никто из школьников): нужно доказать, что если бревно расположено как на рисунке 2, то расстояние от гвоздя A до угла O не меньше 1м.

Это можно сделать так. Расстояние OB (где B - середина бревна) равно 1.5м (половина длины бревна), а расстояние AB равно 0.5м - значит, OA не меньше 1м.

15. В формулировке задачи были допущены ошибки, поэтому результаты по ней не учитывались при определении победителей. Для интересующихся приводим правильную формулировку и решение.

Путешественник отправился из родного города A в самый далёкий от него город B, затем в самый далёкий от B город C и так далее (каждый раз выбирается город, находящийся на наибольшем расстоянии, независимо от того, был ли там уже путешественник или нет; все расстояния между городами попарно различны). Докажите, что либо путешественник попадёт в родной город после двух переходов (из A в B, а затем обратно в A), либо не вернётся в него никогда.
Решение. Предположим, что второй переход был в город C, отличный от A. Тогда расстояние между B и C больше, чем от A до B, и, значит, больше, чем расстояние от A до любого города. Заметим, что с каждый переход путешественника не короче, чем предыдущий (всегда можно вернуться обратно, если нет более далёких городов). Поэтому все переходы, начиная со второго, не меньше, чем расстояние от B до C. Следовательно, ни один из этих переходов не может вести в A (так как расстояние от A до всех городов меньше, чем от B до C). Значит, в этом случае путешественник никогда не вернётся в A.

16. По кругу написано 100 чисел, и каждое равно среднему арифметическому (полусумме) двух соседей. Докажите, что все числа равны.
Решение. Рассмотрим самое большое из чисел (любое, если их несколько). Каждое из стоящих рядом с ним чисел не больше, а их полусумма равна этому числу - значит, каждое из чисел рядом с наибольшим равно наибольшему. Рядом с ними также должны стоять числа, равные наибольшему и т.д. Эта "волна" рано или поздно захватит все числа. Следовательно, все они равны наибольшему.

17. Разность двух целых чисел умножили на их произведение. Могло ли получиться число 12345 ?
Решение. Нет. Оба числа должны быть нечётны (иначе указанное произведение было бы чётным, а 12345 - нечётное число) - но тогда их разность чётна, и произведение опять же должно быть чётным.

18. Брюнеты, составляя 1/3 населения страны (остальные - блондины), выпивают 4/5 всего выпиваемого в стране кефира. Статистики подсчитали, сколько литров кефира в день выпивает средний брюнет, и сколько - средний блондин. Во сколько раз первое число больше второго?
Решение. Ответ: в 8 раз. Пусть x блондинов выпивают в день y литров кефира (т.е. средний блондин выпивает y/x литров кефира в день). Тогда 2x брюнетов выпивают в день y/4 литров кефира (т.е. средний брюнет выпивает (y/4)/(2x)=y/(8x) литров кефира в день). Дробь y/x в 8 раз больше, чем y/(8x).

19. Придумать семизначное число, первая цифра которого равна числу нулей в его десятичной записи, вторая - числу единиц, третья - числу двоек, четвёртая - троек,..., седьмая - числу шестёрок.
Решение. Ответ: 3211000.

20. Какое максимальное количество натуральных чисел от 1 до 60 можно выбрать, чтобы среди них не было отличающихся ровно в два раза?
Решение. Рассмотрим для каждого нечётного числа от 1 до 59 все числа, которые получаются из него умножением на степени двойки: {1,2,4,8,16,32}; {3,6,12,24,48}; {5,10,20,40}; {7,14,28,56}; {9,18,36}; {11,22,44}; {13,26,52}; {15,30,60}; {17,34}; {19,38}; {21,42}; {23,46}; {25,50}; {27,54}; {29,58}; {31}; {33}; {33}; {35}; {37}; {39}; {41}; {43}; {45}; {47}; {49}; {51}; {53}; {55}; {57}; {59} (последние группы состоят из одного числа). Из первой и второй группы можно выбрать максимум по 3 числа (иначе будут выбраны два соседних, которые отличаются в 2 раза), из третьей, четвёртой, пятой, шестой, седьмой и восьмой - максимум по два числа, из остальных 22 групп - максимум по одному. Всего получается не более 3x2+2x6+22=40 чисел. Легко указать способ выбрать ровно столько чисел.

21. За завтраком каждый выпил по чашке кофе с молоком, причём Дима выпил пятую часть всего выпитого молока и восьмую часть всего выпитого кофе. Сколько человек могло участвовать в завтраке? (Все чашки одинаковы, но пропорции молока и кофе в них могут быть разными.)
Решение. Пусть Дима выпил М молока и К кофе (всего К+М). Тогда общий объём выпитого кофе с молоком составляет 5К+8М. Это меньше, чем 8(К+М), и больше, чем 5(К+М). Значит, в завтраке участвовало менее 8 человек и более 5. Примеры, когда участников было 6 или 7, легко привести.
Замечание. Случаи 5 и 8 участников завтрака возможны, если допустить, что в Диминой чашке было только молоко или только кофе.

22. В строчку выписано 20 чисел. Может ли оказаться так, что сумма любых трёх соседних чисел положительна, а сумма всех 20 чисел отрицательна?
Решение. Да. Например, -4,-4,9,-4,-4,9,-4,-4,9,-4,-4,9,-4,-4,9,-4,-4,9,-4,-4,9,-4,-4. Сумма любых трёх соседних чисел равна 1, а сумма всех 20 чисел равна (-2).

23. Тот же вопрос, если числа записаны по кругу.
Решение. Нет. Сложив суммы чисел во всех 20 возможных тройках, мы получим положительное число. Но в эту сумму каждое из 20 чисел входит трижды - поэтому сумма всех чисел есть третья часть от суммы всех троек, и, значит, также положительно.

24. Сколько существует семизначных чисел, составленных из цифр 1 и 2, в которых никакие две единицы не стоят рядом?
Решение. Ответ: 34 (считая число из одних двоек). Это число можно подсчитать непосредственно, а можно и более простым способом. Обозначим через a(n) количество n-значных чисел с таким свойством (n=1,2,...). Любое n-значное число имеет либо вид *2 (где * - (n-1)-значное число), либо *21 (где * - (n-2)-значное число), причём каждое число можно представить так ровно одним способом, и из всех (n-1)- и (n-2)-значных чисел (с указанным свойством) получаются n-значные числа с тем же свойством. Значит, a(n)=a(n-1)+a(n-2). Ясно, что a(1)=2, a(2)=3, откуда a(3)=5, a(4)=8, a(5)=13, a(6)=21, a(7)=34.
Замечание. Если считать, что в числе должна быть хотя бы одна единица, то ответ будет на 1 меньше (33 числа). Однако в условии об этом не сказано.

25. Прямоугольник 30x1 разбит на 30 квадратов. В крайних квадратах стоят белая и чёрная шашки. Они ходят по очереди, передвигаясь в любую из соседних клеток (если она свободна). Начинают белые. Проигрывает тот, кто не может сделать ход. Могут ли чёрные проиграть?
Решение. Единственная позиция, в которой чёрные не могут сделать ход - когда чёрная шашка стоит на самой правой клетке, а белая шашка на соседней (второй справа) клетке. Покажем, что такая позиция не может возникнуть после хода белых. Пронумеруем клетки (слева направо) числами от 1 до 30. После каждого хода белых шашки стоят на клетках, номера которых имеют одну и ту же чётность (либо оба нечётны, либо оба чётны); действительно, после первого хода белых это верно, а затем после каждых двух ходов шашки меняют чётность своих клеток. А в позиции, указанной выше, клетки с белой и чёрной шашкой имеют разную чётность (29 и 30).
Замечание. Многие школьники указывали, что чёрные могут выиграть (и приводили выигрышную стратегию). Однако это не даёт ответа на вопрос задачи: может быть, чёрные могут проиграть, если не будут этой стратегии следовать. На самом деле чёрные никогда не могут проиграть (даже если заранее договорятся с белыми и будут вместе к этому стремиться)!