Рис. 1.
Заочная физико-математическая олимпиада МФТИ рассчитана на учащихся 10-11 классов, но в ней могут участвовать и девятиклассники. Победители олимпиады пользуются правом преимущественного зачисления в МФТИ при прочих равных условиях.
Решение задач оценивается как отличное, а участник олимпиады признается ее победителем с вручением диплома, если решено без ошибок не менее 5-ти любых задач из предложенных 16-ти.
Решения задач должны быть представлены в тонкой ученической тетради, на бложке которой наклеивается анкета участника, где указывается полный почтовый адрес и телефон участника, номер и адрес школы, класс, фамилии, имена и отчества директора школы, учителей физики и математики.
Решения задач необходимо отослать по адресу:
141700, Московская обл., г. Долгопрудный, Институтский пер., д. 9, МФТИ, "Физтех-центр" - не позднее 30 января 2000 года.
Оргкомитет физико-математических олимпиад МФТИ
| Справки можно получить, обратившись в: | |
| Межвузовский центр довузовского образования "Физтех-центр" | (095) 408-64-36 www.abitur.mipt.ru E-mail: abitur@mipt.ru |
| Заочную физико-техническую школу при МФТИ | (095) 408-51-45 |
| Приемную комиссию | (095) 408-48-00 |
| Фамилия | Имя | ||
| Отчество | Учитесь ли в ЗФТШ? (личный номер) | ||
| Класс | Школа | ||
| Индекс | Область | ||
| Район | Город | ||
| Улица | Дом | ||
| Квартира | Телефон | ||
| E-mail и/или интернет | |||
| Математика | (ФИО) |
| Физика | (ФИО) |
| Индекс | Область | ||
| Район | Город | ||
| Улица | Дом | ||
| Тел. | ФИО директора |
| Математика | М-1 | М-2 | М-3 | М-4 | М-5 | М-6 | М-7 | М-8 | М-9 | |
| оценки | ||||||||||
| Физика | Ф-1 | Ф-2 | Ф-3 | Ф-4 | Ф-5 | Ф-6 | Ф-7 | Ф-8 | Ф-9 | |
| оценки |
М-1. Расставьте в вершинах пятиугольника действительные числа так, чтобы сумма чисел на концах некоторой стороны была равна 1, на концах некоторой другой стороны была равна 2, ..., на концах последней стороны равна 5.
М-2. Найдите все значения параметра a, при которых один из корней уравнения x2 + (sin a)x + cos a = 0 равен синусу, а другой - косинусу некоторого угла.
М-3. Найдите натуральное число n такое, чтобы суммы цифр чисел n и n+1 делились на 1999.
М-4. Найдите все действительные числа p такие, что неравенство px2>(x-p)1/2 выполняется при всех x>p.
М-5. Дана окружность с хордами AB=4, BC=6. Найдите ее радиус, если известно, что длина хорды данной окружности, параллельной BC и проходящей через середину AB, равна 5.
М-6. Решите систему уравнений:
| { | (0,5+x1)1/2+ | (0,5+x2)1/2... | (0,5+x10)1/2=8 |
| (0,5-x1)1/2+ | (0,5-x2)1/2... | (0,5-x10)1/2=6 |
М-7. Десять волейбольных команд сыграли между собой турнир в один круг. За выигрыш давалось одно очко, за проигрыш - нуль. Пусть an - количество очков, набранных командой, занявшей n-ое место; n=1,2,...,10. Какое наименьшее значение может принять сумма a1+2a2+...+10a10.
М-8. На отрезке AC взята точка B, отличная от A и C. Рассматриваются все возможные окружности S, проходящие через точки A и B. Из точки C к каждой из таких окружностей проводится по две касательные; обозначим K(S) и L(S) точки касания. Найдите геометрическое место точек - середин отрезков KL.
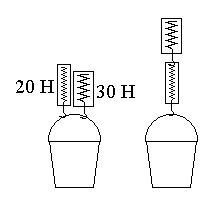
Ф-1. Ведро с фруктами взвешивают на двух разных пружинных весах. Первый раз ведро подвесили на параллельно расположенные весы, второй раз - на последовательно расположенные (см. рис. 1). В первом случае весы показали 20 Н и 30 Н. Что показали весы во втором случае.

Рис. 1.
Ф-2. В стакан с водой бросили стальной шарик объемом V=1,5 см3. На какую величину увеличилось давление вблизи дна? Площадь внутреннего поперечного сечения стакана S=30 см2, его стенки вертикальны (рис. 2).
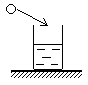
Рис. 2.
Ф-3. В цилиндрическом сосуде, стоящем на столе в комнате, находится под поршнем воздух (см. рис. 3). Масса поршня m=1 кг. его площадь S=50 см2. Трением поршня о стенки сосуда пренебречь. На поршень поставили гирю массой M=6 кг. Оценить, во сколько раз уменьшился объем воздуха в сосуде после наступления теплового равновесия. Примечание: будьте внимательны!
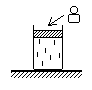
Рис. 3.
Ф-4. Состав из локомотива и одинаковых вагонов отходит от станции, набирая скорость. Сила натяжения сцепок между четвертым и пятым вагонами (считая от локомотива) в 3 раза больше, чем между четырнадцатым и пятнадцатым. Сколько вагонов в составе? Сила сопротивления движению отсутствует.
Ф-5. В схеме (см. рис. 4) R1=20 Ом. При каком значении R2 конденсатор не будет заряжен. Внутреннее сопротивление источников не учитывать.
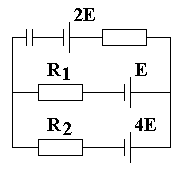
Рис. 4.
Ф-6. Доска с лежащим на ней бруском совершает колебания с амплитудой A = 8 см и перидом T = 0,8 с вдоль прямой на гладкой горизонтальной поверхности стола под действием упругой пружины (см. рис. 5). При каких значениях коэффициента трения скольжения между бруском и доской брусок не будет двигаться по доске?
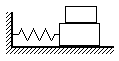
Рис. 5.
Ф-7. В вершинах равностороннего треугольника со стороной a удерживаются небольшие по размерам шарики с зарядами q каждый и массами M, M и m, причём m<<M (рис. 6). Шарики одновременно отпускают.
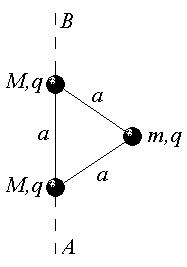
Рис. 6.
1. Найти скорости (по модулю) шариков после их разлета., т. е. после удаления их на бесконечно большое расстояние друг от друга.
2. Под каким углом a к линии AB будут двигаться шарики после разлета?
Ф-8. На гладком столе лежит пружина длиной l0 с числом витков N. К концам пружины с помощью гибких проводов подсоединили источник тока с эдс E и внутренним сопротивлением r. В результате установившаяся длина пружины стала 0,75l0, а площадь поперечного сечения S. Найти механическую жесткость пружины, если ее электрическое сопротивление R. Пружину можно считать соленоидом. Индуктивность соленоида находится по формуле L=m0n2S/l, где l - длина соленоида, N - число витков, S - площадь поперечного сечения, m0 - магнитная постоянная.