Заключительный этап
1999/2000 учебный год
Пермь, 19-26 апреля 2000 г.
Комплект задач подготовлен методической комиссией по физике Центрального оргкомитета Всероссийских олимпиад школьников Министерства образования РФ.
Задача 1.
К диску радиуса R, насаженному на горизонтальный вал мотора, под действием силы тяжести прижимается тяжёлый брусок массой M. Брусок может свободно поворачиваться относительно оси O (см. рис.). Длина бруска равна L, его толщина h. Точка соприкосновения бруска с диком находится на расстоянии l от левого края бруска. Коэффициент трения скольжения между бруском и диском равен m. Предполагая, что мотор может развивать мощность P, определите угловую скорость w вращения диска в зависимости от величины l. Рассмотрите случаи вращения диска по (w+) и против (w-) часовой стрелки. Постройте качественные графики w+(l) и w-(l).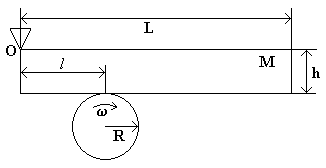
Задача 2.
Кот Леопольд стоял у края крыши сарая. Два злобных мышонка выстрелили в него из рогатки. Однако, камень, описав дугу, через t1=1,2 с от наклонного ската крыши сарая у самых лап кота и через t2=1,0 с попал в лапу стрелявшего мышонка (см. рис.). На каком расстоянии S от мышей находился кот Леопольд?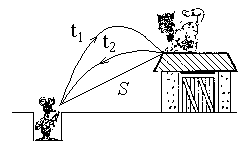
Задача 3.
Известно, что дистиллированную воду, очищенную от примесей, можно охладить без превращения в лёд ниже температуры t0=0oC. В зависимости от внешнего давления процесс кристаллизации воды может начаться при некоторой температуре t1<t0. Образовавшийся при этом лёд отличается по своим физическим свойствам от обычного льда при температуре 0oC. Определите, чему равна удельная теплота плавления льда (l2) при температуре t1=-10oC. Удельную теплоёмкость воды в интервале температур от -10oC до 0oC примите равной c1=4,17*103 Дж/(кг*K). Удельную теплоёмкость льда в этом интервале температур примите равной c2=2,17*103 Дж/(кг*K). Удельная теплота плавления льда при температуре 0oC равна l1=3,32*105 Дж/кг.Задача 4.
Дан "чёрный ящик" с тремя выводами. Известно, что внутри ящика находится некоторая схема, составленная из резисторов (см. рис.). Если к выводам (1),(3) подключить источник напряжения U=15 В и измерить с помощью вольтметра напряжения между выводами (1),(2) и (2),(3), то они оказываются равными U12=6 В и U23=9 В. Если источник напряжения подключить к выводам (2),(3), то U21=10 В и U13=5 В. Какими будут напряжения U13, U32, если источник подключить к выводам (1), (2)? Нарисуйте возможные схемы "черного ящика" с минимальным числом резисторов. Полагая, что наименьшее сопротивление из всех резисторов равно R, найдите сопротивления остальных резисторов.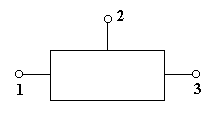
Задача 1.
На гладкой горизонтальной поверхности коллеблется на пружине вдоль оси Ox брусок. По направлению к бруску вдоль оси Ox движется по направлению к бруску со скоростью v0 шарик (см. рис. 1), который после упругого удара о брусок отскакивает в противоположном направлении. Масса шарика во много раз меньше массы бруска. График зависимости координаты x бруска от времени t представлен на рис. 2.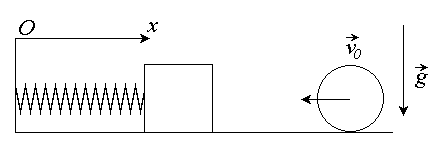
Рис. 1
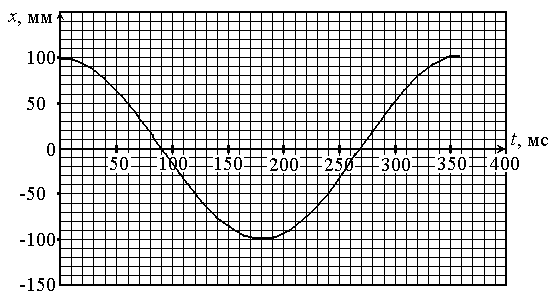Рис. 2
Задача 2.
Длинный товарный поезд трогается с места. Вагоны соединены друг с другом с помощью абсолютно неупругих сцепок. Первоначальный зазор в каждой сцепке равен L (см. рис.). Масса локомотива равна m, а его порядковый номер - первый. Все вагоны загружены, и масса каждого из них тоже равна m.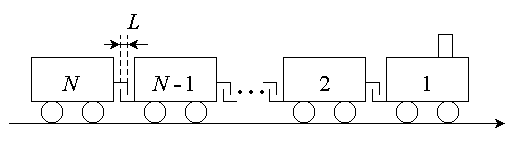
Задача 3.
В воду массы m бросают вещество такой же массы, обладающее следующими свойствами: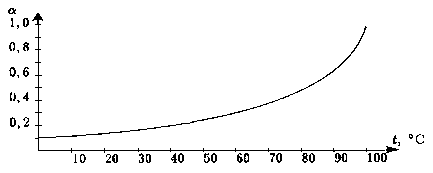
Задача 4.
Кривая ABC (см. рис.) является адиабатой для некоторого вещества, у которого внутренняя энергия зависит от произведения p*V, т. е. U=U(pV). Найдите полное количество тепла, которое тело получило в процессе 1-2, изображённом на рис.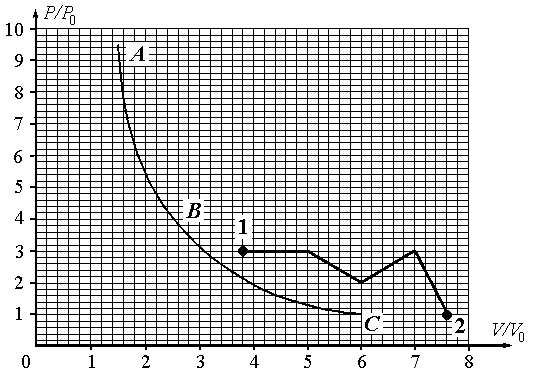
Задача 5.
В электрической цепи, представленной на рисунке, ключ K разомкнут и токи не текут. Определите: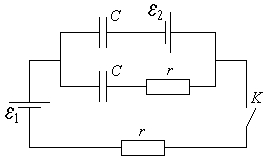
Задача 1.
На два вращающихся в противоположных направлениях цилиндрических валика радиусом R=0,5 м положили длинный однородный брус (см. рис.) так, что его центр масс оказался смещённым от оси симметрии на aL, где a=3/8, а L=2 м - расстояние между осями валиков. Затем брус без толчка отпускают. Коэффициент трения между брусом и валиками равен k=0,3 и не зависит от их относительной скорости. Угловая скорость вращения валиков равна w1=10 с-1. После того, как колебания установились, угловую скорость вращения валиков уменьшили в 10 раз. Найдите частоту W и амплитуду A2 новых установившихся колебаний бруса.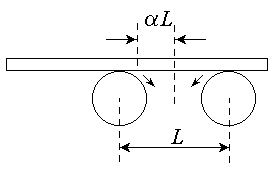
Задача 2.
К двум точкам A и B, находящимся на одной горизонтали, между которыми расстояние 2a, прикреплена тонкая лёгкая нерастяжимая нить длиной 2l (см. рис. 1). По нити без трения скользит маленькая тяжёлая бусинка. Ускорение свободного падения g.Примечание: при решении задачи Вам может оказаться полезной формула
(1+x)1/2 ~ 1+(1/2)x+(1/8)x2+..., при x<<1
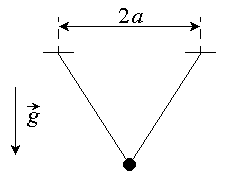Рис. 1
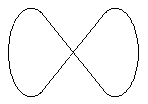Рис. 2
Задача 3.
Кривая ABC (см. рис.) является адиабатой для некоторого вещества, у которого внутренняя энергия зависит от произведения p*V, т. е. U=U(pV). Найдите полное количество тепла, которое тело получило в процессе 1-2, изображённом на рис.
Задача 4.
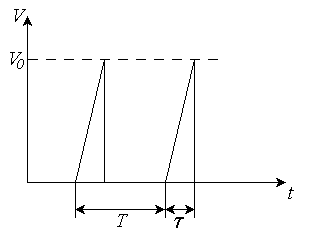
В электростатическом вольтметре сила притяжения между металлическими пластинами плоского конденсатора C измеряется с помощью аналитических весов (см. рис. 1). При постоянном напряжении V1=500 В между пластинами 1 и 2 весы уравновешиваются разновесом массой m1=200 мг. На пластины конденсатора подаётся периодическая последовательность треугольных импульсов напряжения с длительностью t=5*10-4 с и периодом повторения T=0,01 с (см. рис. 2). Чему равна амплитуда импульсов V0, если в этом случае весы уравновешиваются разновесом массой m2=30 мг. Период собственных колебаний весов много больше T.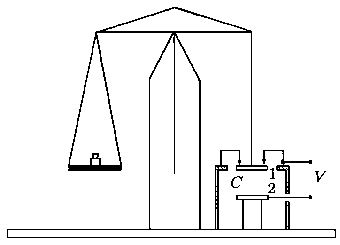
Задача 5.
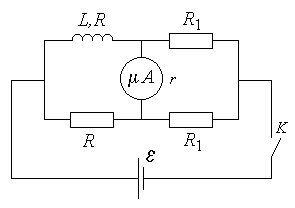
В электрической цепи с мостиком Уинстона, изображённой на рис., после установления всех токов замыкают ключ K. Определите, при какой величине сопротивлений R1 через микроамперметр с внутренним сопротивлением r после замыкания ключа K протечёт наибольший заряд Q. Все остальные параметры электрической цепи, указанные на рисунке, считать заданными. Внутренним сопротивлением источника напряжения и сопротивлением соединительных проводов пренебречь.