Ответ: 121.
1. Решите ребус:
***
***
---
*6*
*6*
7**
-----
*****
Ответы: 187*433, 123*677, 123*637, 261*311, 361*211, 761*111.
2. Решите ребус:
**3
5**
---
*7*
***
***
-----
*****
Ответы: 173*511, 173*521, 173*531, 173*541, 173*551, 143*514, 143*524,
143*534, 143*544, 143*554, 143*564, 113*516, 113*526, 113*536, 113*546,
113*556, 113*566, 113*576, 113*586, 163*516, 163*526, 163*536, 163*546,
163*556, 163*566, 193*513, 193*514.
3. Фермер Егор купил овцу, которая тут же родила овечку. С тех пор
каждый следующий год эта овца приносила по одной овечке. Каждая родившаяся
овца через три года также начинает приносить по одной овечке в год. Допустим,
что овцы бессмертны, а фермер их не продает и не режет. Сколько овец будет в
его отаре через 15 лет после покупки?
Ответ: 595. (Екатеринбург, область, 1993, 10 кл.)
4. Сумма всех попарных произведений трех натуральных чисел равна 27.
Чему может равняться сумма самих этих чисел?
Ответы: 15, 10, 9 (что соответствует тройкам
(1,1,13), (1,3,6), (3,3,3) ).
5. На контуре квадрата отмечены 32 точки: 4 вершины, а также по 7
точек на каждой стороне, делящих ее на 8 равных частей. Сколько существует
равнобедренных треугольников с вершинами в отмеченных точках?
Ответ: 216.
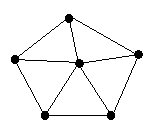
6. Во дворе дома вкопали шесть столбов и натянули между веревки так,
как показано на рисунке справа. Сколькими различными способами можно снять пять
веревок так, чтобы по оставшимся веревкам можно было добраться от любого столба
до любого другого?

Ответ: 121.
7. Найдите как можно большее натуральное число, в записи которого не
встречается цифра 0, которое делится на сумму своих цифр, причем любое число,
получаемое из него отбрасываеием одной или нескольких последних цифр, обладает
тем же свойством.
Ответы: 126, 18, 216, 243, 24786, 27, 364, 423, 45, 481, 486, 54,
63, 72, 81, 8463.
8. Найдите как можно больше имен существительных (нарицательных, ед. числа, именительного падежа), у которых все буквы расположены в алфавитном порядке.
9. Выразите как можно больше последовательных натуральных чисел, начиная с 1, используя только цифру 2 и скобки (в неограниченном количестве), операцию возведения в степень (в неограниченном количестве) и не более четырех знаков арифметических действий.