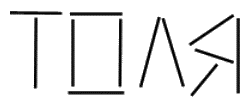
1. (исходная) Какого числа какого месяца до наступления 1999 года останется 1519 часов?
2. (исходная) Переложите одну спичку так, чтобы получилось женское
имя:
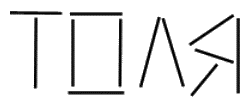
3. (исходная) Представьте число 1998 в виде суммы нескольких последовательных натуральных чисел.
4. (исходная) Найдите хотя бы одно решение ребуса КОЛ*КОЛ = ПРИКОЛ (одинаковыми буквами обозначены одинаковые цифры, разными - разные).
5. (исходная) Город А и город Б находятся на берегу озера "Клякса". Петя по берегу из А в Б доходит за 48 минут. По озеру на лодке Петя может перемещаться в 6 раз медленнее, чем по берегу, но этот путь в 8 раз короче. За какое время Петя может добраться по воде из А в Б?
6. (исходная) Число КУБ является кубом целого числа, а число БУК - простое. Какие это числа?
7. (исходная) Чебурашка и Гена делили одно и то же число с остатком. Чебурашка на 8, Гена - на 9. Неполное частное, которое получил Чебурашка, в сумме с остатком от деления, который получил Гена, дали 13. Какой остаток при делении получился у Чебурашки?
8. (исходная) В полдень из города А по местному времени в город Б вылетел самолет, совершил там посадку в 17 часов местного времени и отправился обратно в 21 час местного времени. Самолет вернулся в город А в 10 утра местного времени города А. Сколько часов длится перелет самолета между городами?
9. (исходная) Запишите все натуральные числа от 1 до 13 в строку так, чтобы каждое число, начиная со второго, являлось делителем суммы предыдущих.
10. (исходная) Пете и Васе вместе 35 лет. При этом Васе вдвое больше лет, чем было Пете тогда, когда Васе было столько лет, сколько Пете сейчас. Сколько лет Пете?
11. (исходная) Расставьте по кругу четыре единицы, три двойки и три тройки так, чтобы сумма любых трех подряд стоящих цифр не делилась на 3.
12. (исходная) Если у четырехзначного числа, являющегося полным квадратом, отбросить первую цифру, то оно станет кубом некоторого числа, а если после этого отбросить и вторую, то останется четвертая степень целого числа. Найдите это четырехзначное число.
13. (исходная) Решите ребус, заменив одинаковые буквы одинаковыми цифрами, а разные - разными: РОЗА+ОЗА+ЗА+А=2000
14. (исходная) По дороге мимо наблюдателя проехали через равные промежутки времени автобус, мотоцикл и автомобиль. Мимо другого наблюдателя они проехали с такими же промежутками времени, но в другом порядке: автобус, автомобиль и мотоцикл. Найдите скорость автобуса, если скорость автомобиля 60 км/ч, мотоциклиста - 30 км/ч.
15. (исходная) Как фигуру, показанную на рисунке, разрезать по
нарисованным линиям на 11 одинаковых частей?

1. (зач. мл.) Отец и сын катаются по кругу на катке. Время от времени отец обгоняет сына. Когда сын стал двигаться по кругу в противоположном направлении, они стали встречаться в 5 раз чаще. Во сколько раз отец бегает на коньках быстрее своего сына?
2. (зач. мл.) Найдите наименьшее натуральное число, вычеркиванием цифр из записи которого, можно получить запись любого натурального числа от 1 до 31.
3. (зач. мл.) Как вырезать наибольшее количество прямоугольников 1*7 из прямоугольника 26*11 ?
4. (зач. мл.) Каких пятизначных натуральных чисел больше: не делящихся на 5 или тех, у которых первая и вторая цифры слева - не пятерки?
5. (зач. мл.) Найдите отношение площади закрашенного треугольника к площади большого квадрата, если известно, что сторона большого квадрата втрое длиннее стороны малого.
7. (зач. мл.) Первого апреля на птичьем рынке можно было обменять 3-х удавов на 5 мартышек и 7 попугаев, 2-х слонов на 7 мартышек и 5 попугаев, а 9 мартышек - на 2 удавов и 1 слона. А на сколько удавов и слонов можно было обменять 36 попугаев?
6. (зач. мл.) Среди двузначных чисел найдите все такие, которые не делятся на 13, и которые не будут делиться на 13, если даже в их записи заменить одну из цифр (при этом первую цифру заменять на 0 нельзя).
8. (зач. мл.) Найдите хотя бы одно решение ребуса 15*два=6*пять . (разные буквы - разные цифры)
9. (зач. мл.) Было 100 кг грибов влажностью 98%. После сушки их влажность понизилась до 90%. Сколько стали весить грибы после сушки?
10. (зач. мл.) Знайка хочет составить число из различных цифр так, чтобы любые две стоящие подряд цифры образовывали простое число. Какое наибольшее число он может получить?
11. (зач. мл.) Какое число стоит на 1998 месте в последовательности чисел: 1; 2; 2; 3; 3; 3; 4; 4; 4; 4; 5;:?
12. (зач. мл.) На доске было записано число х с одним знаком после запятой, а под ним в столбик числа х+0,1; х+0,2; х+0,3 и х+0,4. Вова стер все знаки после запятых (вместе с запятыми) в записи этих чисел и подсчитал сумму, которая оказалась равной 33. Найдите х.
13. (зач. мл.) Вова обнаружил, что в 1998 году возраст его старшего брата равен сумме цифр года рождения (брата). Сколько лет исполнилось в 1998 году старшему брату Вовы?
14. (зач. мл.) На доске записали 8 двузначных чисел, дающих все возможные остатки при делении на 8. Какое наименьшее количество различных цифр могло быть при этом использовано? Приведите пример.
15. (зач. мл.) Коля и Витя, гуляя по парку, набрели на круглую поляну, обсаженную дубами. Коля пошел вокруг поляны, считая деревья. Витя сделал то же, но начал с другого дерева. Дерево, которое было у Коли под номером 31, у Вити было 13, а 13 - 35. Сколько дубов росло вокруг поляны?
16. (зач. мл.) Чему равна сумма цифр куба числа, записанного тысяча девятьсот девяноста восемью девятками?
17. (зач. мл.) Как фигуру, показанную на рисунке, разрезать по
нарисованным линиям на 11 одинаковых частей?

18. (зач. мл.) Расшифруйте фразу:
МУТМИТ ЮКЫВ ТАРЕНАРИНОХ
Какой шифр в этой задаче?
1. (зач. ст.) Отец и сын катаются по кругу на катке. Время от времени отец обгоняет сына. Когда сын стал двигаться по кругу в противоположном направлении, они стали встречаться в 5 раз чаще. Во сколько раз отец бегает на коньках быстрее своего сына?
2. (зач. ст.) Найдите наименьшее натуральное число, вычеркиванием цифр из записи которого, можно получить запись любого натурального числа от 1 до 31.
3. (зач. ст.) Как вырезать наибольшее количество прямоугольников 1*7 из прямоугольника 26*11 ?
4. (зач. ст.) Каких пятизначных натуральных чисел больше: не делящихся на 5 или тех, у которых первая и вторая цифры слева - не пятерки?
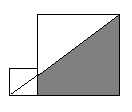
5. (зач. ст.) Найдите отношение площади закрашенного четырехугольника
к площади большого квадрата, если известно, что сторона большого квадрата
втрое длиннее стороны малого.
6. (зач. ст.) Среди двузначных чисел найдите все такие, которые не делятся на 13, и которые не будут делиться на 13, если даже в их записи заменить одну из цифр (при этом первую цифру заменять на 0 нельзя).
7. (зач. ст.) Первого апреля на птичьем рынке можно было обменять 3-х удавов на 5 мартышек и 7 попугаев, 2-х слонов на 7 мартышек и 5 попугаев, а 9 мартышек - на 2 удавов и 1 слона.. А на сколько удавов и слонов можно было обменять 36 попугаев?
8. (зач. ст.) Найдите хотя бы одно решение ребуса 15*два=6*пять. (разные буквы - разные цифры)
9. (зач. ст.) Было 100 кг грибов влажностью 98%. После сушки их влажность понизилась до 90%. Сколько стали весить грибы после сушки?
10. (зач. ст.) Знайка хочет составить число из различных цифр так, чтобы любые две стоящие подряд цифры образовывали простое число. Какое наибольшее число он может получить?
11. (зач. ст.) Какое число стоит на 1998 месте в последовательности чисел: 1; 2; 2; 3; 3; 3; 4; 4; 4; 4; 5; ...?
12. (зач. ст.) На доске было записано число х с одним знаком после запятой, а под ним в столбик числа х+0,1; х+0,2; х+0,3 и х+0,4. Вова стер все знаки после запятых (вместе с запятыми) в записи этих чисел и подсчитал сумму, которая оказалась равной 33. Найдите х.
13. (зач. ст.) Как разделить треугольник n-звенной ломаной, выходящей из какой-либо вершины треугольника, на n+1 равных по площади треугольников (см. рис.) ?
14. (зач. ст.) Вова обнаружил, что в 1998 году возраст его старшего брата равен сумме цифр года рождения (брата). Сколько лет исполнилось в 1998 году старшему брату Вовы?
15. (зач. ст.) На доске записали 8 двузначных чисел, дающих все возможные остатки при делении на 8. Какое наименьшее количество различных цифр могло быть при этом использовано? Приведите пример.
16. (зач. ст.) Коля и Витя, гуляя по парку, набрели на круглую поляну, обсаженную дубами. Коля пошел вокруг поляны, считая деревья. Витя сделал то же, но начал с другого дерева. Дерево, которое было у Коли под номером 31, у Вити было 13, а 13 - 35. Сколько дубов росло вокруг поляны?
17. (зач. ст.) Чему равна сумма цифр куба числа, записанного тысяча девятьсот девяноста восемью девятками?
18. (зач. ст.) В равнобочной трапеции АВСD проведены высота
ВН и и диагональ ВD, которая оказалась биссектрисой угла
CDA (см. рис.). Угол АВН на 30o больше угла
СВD. Найдите угол HBD.
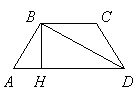
19. (зач. ст.) Найдите все натуральные числа, которые равны удвоенной сумме некоторых двух своих различных делителей.
20. (зач. ст.) Расшифруйте фразу:
МУТМИТ ЮКЫВ ТАРЕНАРИНОХ
Какой шифр в этой задаче?