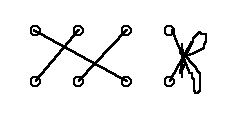
1. Решите в натуральных числах уравнение (n! - 1)2=m! + 1
2. В противоположных углах прямоугольной комнаты положили два одинаковых прямоугольных ковра. Площадь их общей части оказалась равна 5 м2. Затем оба ковра развернули в своих углах на 90 градусов. Площадь общей части стала равна 2 м2. Найдите, на сколько длина ковра больше его ширины, если длина комнаты больше ширины комнаты на 1,5 м?
3. На шахматной доске отметили 15 клеток. Докажите, что среди них есть две такие, что с одной на другую конь может попасть не более чем за два хода.
4. Есть чашечные весы, кран и три одинаковых, достаточно вместительных сосуда без разметки. В один сосуд налито 7 л воды, в другой - 10 л, а третий пуст. Разрешается ставить два сосуда на весы и доливать в один из них воду (из крана или третьего сосуда), пока весы не уравновесятся. Можно также переливать всю воду из одного сосуда в другой и выливать воду из сосуда в раковину. Как отмерить 19 л воды в одном из сосудов?
5. На стороне BC выпуклого четырехугольника ABCD лежит такая точка M, что AB = BM и MC = CD. Известно, что /AMD = 90o. Докажите, что произведение площадей треугольников ABM и CDM вчетверо меньше квадрата площади треугольника AMD.
6. Обозначим через A количество способов раскрасить прямоугольник 6*8 в восемь цветов так, чтобы в каждой строке и каждом столбце все цвета были различны, а через B - количество способов раскрасить по этим же правилам прямоугольник 7*8. Что больше: 2А или В?
7. Найти наибольшее число, кратное 27, в записи которого каждая цифра встречается не более одного раза.
8. В чашку налили 20 ложек кофе. Саша выпивает из чашки одну ложку кофе и добавляет одну ложку молока. Перемешивает. Затем выпивает одну ложку смеси и опять доливает ложку молока. Может ли Саша, проделав такую операцию несколько раз, получить смесь, состоящую наполовину из кофе и наполовину из молока?
1. Прямоугольный параллелепипед разделен тремя плоскостями на 8 частей в форме прямоугольного параллелепипеда каждая. За один вопрос можно узнать объем одной из частей. За какое наименьшее число вопросов можно узнать объем исходного параллелепипеда?
2. Докажите, что уравнение (a - b)2 = НОК(a, b) имеет бесконечно много решений в натуральных числах.
3. Дан параллелограмм ABCD. Обозначим через R радиус описанной окружности треугольника АВС. Пусть Н - точка пересечения высот треугольника АВС (треугольник АВС - остроугольный). Найдите расстояние HD.
4. Сколькими способами можно расставить на клетчатой доске 100*100 черные и белые фишки по одной на каждой клетке, чтобы никакие три одноцветные фишки не располагались подряд по горизонтали, вертикали или диагонали?
5. Докажите, что если числа a, b, c и d принадлежат отрезку [1; 2], то ((a+b)/(b+c))+((c+d)/(d+a)) < 4/9 .
6. На доске записано число 1998. Двое по очереди приписывают к нему по одной цифре: первый - слева и только нечетные цифры, второй - справа и только четные цифры. Выигрывает тот, после хода которого число впервые становится кратным 11. Кто из игроков может при правильной игре обеспечить себе выигрыш?
7. Комиссия состоит из 49 человек. В каждом заседании участвуют ровно три члена комиссии. Можно ли составить расписание работы комиссии так, чтобы любые два члена комиссии встретились на заседаниях ровно один раз?
8. Есть пять монет достоинством 1, 2, 3, 5 и 10 ижиков. Четыре из них - настоящие, их вес в граммах равен их достоинству, а одна - фальшивая, ее вес в граммах не равен ее достоинству. Как, используя только чашечные весы без гирь, найти фальшивую монету?
1. На всех черных клетках шахматной доски размером 4*4 стоит по коню. Сколькими различными способами они могут одновременно прыгнуть так, чтобы после прыжка все кони снова оказались на разных клетках?
2. В вершинах куба выписаны числа, а на каждом ребре - сумма чисел в его концах. Назовем округлением замену нецелого числа на одно из двух ближайших целых (с недостатком или с избытком), а целое пусть при округлении не меняется. Докажите, что можно все 20 чисел округлить так, чтобы по-прежнему на каждом ребре стояла сумма чисел в его концах.
3. На плоскости нарисованы несколько (не меньше трех) треугольников так, что любые два из них симметричны друг другу относительно некоторой прямой. Докажите, что все нарисованные треугольники - равнобедренные.
4. Клетчатый квадрат 12*12 разбили на прямоугольники из двух клеток так, что между любыми двумя клетками есть путь ладьи, проходящий не более чем по n прямоугольникам. При каком наименьшем n такое разбиение возможно?
5. Последовательность чисел образована по следующему правилу. Первые три ее члена - a1, а2, а3, - произвольные натуральные числа. Четвертый член а4 равен остатку от деления а2а3 на a1, пятый член а5 равен остатку от деления а3а4 на a2 и т.д. Докажите, что в этой последовательности обязательно встретится 0.
6. По кругу записаны 15 различных натуральных чисел. Известно, что для любых двух соседей отношение большего к меньшему - целое число. Могут ли все эти отношения быть меньше 20, но больше 10?
7. Сумма длин двух диагоналей выпуклого пятиугольника больше, чем сумма длин трех других диагоналей. Докажите, что эти две диагонали исходят из одной вершины.
8. Несколько различных натуральных чисел имеют сумму, равную 100. Какое наибольшее значение может иметь их произведение?
1. Имеются два бикфордовых шнура. Каждый горит ровно минуту, но, к сожалению, неравномерно. Можно ли с их помощью отмерить 45 секунд?
2. В племени Мумбо-Юмбо состоялся многокруговой чемпионат по футболу с участием 18 команд. За победу присуждалось 2 очка, за ничью - 1, за поражение - 0. Ознакомившись с результатами чемпионата, вождь повелел считать, что за победу дается 3 очка. Мог ли в результате этого нововведения порядок команд в итоговой таблице измениться на противоположный?
3. Назовем обрезком числа новое число, получаемое стиранием одной или нескольких последовательных начальных цифр данного числа. Найдите наибольшее число, не имеющее в своей записи нулей, которое делится на любой из своих обрезков.
4. За праздничным столом должно собраться 8 человек, и хозяйка режет торт на 8 частей. Она знает, однако, что один из гостей может не прийти, и тогда кому-то достанется два куска торта. Хозяйка хочет, чтобы в обоих случаях наибольшая порция была не более чем в а раз больше наименьшей. При каком наименьшем a она сможет этого добиться?
5. На плоскости даны 1997 точек. Двое по очереди соединяют эти точки отрезками, причем один отрезок нельзя проводить дважды. Проигрывает тот, после хода которого впервые образуется замкнутая ломаная с нечетным числом звеньев. Кто выиграет при правильной игре?
6. Кузнечик прыгает по прямой. Первый его прыжок на один см, второй на два см, ..., k-ый прыжок - на k см в ту или другую сторону. Он совершил 1998 прыжков. Какое наибольшее число раз он мог побывать в исходной точке?
7. Луч света, выйдя из вершины А внутрь зеркального квадрата ABCD, после последовательных отражений от сторон BC, CD, DA, BC, BA и AD попадает в вершину С. Отметим точки, в которых луч отразился от стороны ВС. Найдите длины отрезков, на которые эти точки делят сторону ВС.
8. Найдите все пары целых чисел (х,у), для которых x - 3y = (3x + y)3.
1. Решите в натуральных числах уравнение (n!)2 + n! = m!
2. В противоположных углах квадратной комнаты положили два одинаковых прямоугольных ковра. Площадь их общей части оказалась равна 50 дм2. Затем один из ковров развернули в своем углу на 90 градусов. Площадь общей части стала равна 25 дм2. Найдите, на сколько длина ковра больше его ширины?
3. На шахматной доске отметили 17 клеток. Докажите, что среди них есть две такие, что с одной на другую конь может попасть не более чем за два хода.
4. Есть чашечные весы, кран и три одинаковых, достаточно вместительных сосуда без разметки. В один сосуд налито 7 л воды, в другой - 10 л, а третий пуст. Разрешается ставить два сосуда на весы и доливать в один из них воду (из крана или третьего сосуда), пока весы не уравновесятся. Можно также переливать всю воду из одного сосуда в другой и выливать воду из сосуда в раковину. Как отмерить 19 л воды в одном из сосудов?
5. Вова идет по прямой дороге. Сначала он делает 10 шагов вперед, потом - два шага назад, потом 10 шагов вперед, потом - шаг назад, потом - опять 10 шагов вперед и затем два шага назад, далее снова 10 шагов вперед и шаг назад и т.д. Сколько шагов он сделает к моменту, когда впервые окажется в 1998 шагах от места старта?
6. Обозначим через A количество способов раскрасить прямоугольник 7*8 в восемь цветов так, чтобы в каждой строке и каждом столбце все цвета были различны, а через B - количество способов раскрасить по этим же правилам квадрат 8*8. Что больше: А или В?
7. Внутри параллелограмма ABCD взяли точку O. Докажите, что OA<OB+OC+OD.
8. Найти наибольшее число, кратное 7, в записи которого каждая цифра встречается не более одного раза.
1. Прямоугольник разделен двумя прямыми на четыре части в форме прямоугольников каждая. За один вопрос можно узнать площадь одной из частей. За какое наименьшее число вопросов можно узнать площадь исходного прямоугольника?
2. Натуральные числа a и b, таковы, что (a - b)2 = НОК(a, b). Докажите, что НОД(a, b) > 1.
3. Дан параллелограмм ABCD. Обозначим через R радиус описанной окружности треугольника АВС. Пусть Н - точка пересечения высот треугольника АВС (треугольник АВС - остроугольный). Найдите расстояние HD.
4. Сколькими способами можно расставить на клетчатой доске 8*8 черные и белые фишки по одной на каждой клетке, чтобы никакие три одноцветные фишки не располагались подряд по горизонтали, вертикали или диагонали?
5. Докажите, что если числа a, b, c и d принадлежат отрезку [1; 2], то ((a+b)/(b+c))+((c+d)/(d+a)) < 4/9 .
6. На математическом конкурсе было предложено несколько простых и несколько сложных задач. Участнику давали 3 очка за решение сложной задачи и 2 очка - за решение простой задачи. Кроме того, за каждую нерешенную простую задачу снималось одно очко. Рома решил 10 задач и набрал 14 очков. Сколько простых задач было предложено на конкурсе?
7. Есть пять монет достоинством 1, 2, 3, 5 и 10 ижиков. Четыре из них - настоящие, их вес в граммах равен их достоинству, а одна - фальшивая, ее вес в граммах не равен ее достоинству. Как, используя только чашечные весы без гирь, найти фальшивую монету?
8. Шахматный слон ходит по диагонали на любое число клеток. Назовем ход слона нечетным, если слон за этот ход переместился на нечетное число клеток. Однажды слон, сделав несколько ходов, попал из левого нижнего в правый верхний угол шахматной доски (8*8). Докажите, что он сделал нечетное число нечетных ходов.
1. В вершинах шестиугольника выписаны числа, а на каждой стороне - сумма чисел в ее концах. Назовем округлением замену нецелого числа на одно из двух ближайших целых (с недостатком или с избытком), а целое пусть при округлении не меняется. Докажите, что можно все 12 чисел округлить так, чтобы по-прежнему на каждом ребре стояла сумма чисел в его концах.
2. Даны три точки, не лежащие на одной прямой. Циркулем и линейкой проведите через эти точки три параллельные прямые так, чтобы одна из них находилась на равных расстояниях от двух других.
3. В ряд были выписаны натуральные числа 1, 2, 3,...,n. Их стали записывать в новом порядке: сперва по возрастанию все кратные 2 (то есть 2, 4, 6,...), затем по возрастанию - оставшиеся, кратные 3 (то есть 3, 9, 15,...), далее - оставшиеся, кратные 5, потом - кратные 7 и т.д. В результате число 1997 снова оказалось на 1997-м месте. При каких n это возможно?
4. Для игры в классики на земле нарисован ряд клеток, в которые вписаны по порядку числа от 1 до 10 (см. рис). Маша прыгнула снаружи в клетку 1, затем попрыгала по остальным клеткам (каждый прыжок - на соседнюю по стороне клетку) и выпрыгнула наружу из клетки 10. Известно, что на клетке 1 Маша была 1 раз, на клетке 2 - 2 раза, ..., на клетке 9 - 9 раз. Сколько раз побывала Маша на клетке 10?
| 1 | 4 | 5 | 8 | 9 |
| 2 | 3 | 6 | 7 | 10 |
5. На всех черных клетках шахматной доски размером 4*4 стоит по коню. Сколькими различными способами они могут одновременно прыгнуть так, чтобы после прыжка все кони снова оказались на разных клетках?
6. По кругу записаны 12 различных натуральных чисел. Известно, что для любых двух соседей отношение большего к меньшему - целое число. Могут ли все эти отношения быть меньше 20, но больше 10?
7. Сумма длин двух диагоналей выпуклого пятиугольника больше, чем сумма длин трех других диагоналей. Докажите, что эти две диагонали исходят из одной вершины.
8. В записи трех трехзначных чисел использованы только цифры 1, 8 и 9. Сумма этих чисел равна 1998. Докажите, что если в каждом из них поменять местами первую и последнюю цифры, то их сумма не изменится.
1. Имеются два бикфордовых шнура. Каждый горит ровно минуту, но, к сожалению, неравномерно. Можно ли с их помощью отмерить 45 секунд?
2. В однокруговом турнире по футболу участвует 18 команд, у каждой из которых имеется свой стадион. Какое наибольшее количество туров в турнире можно провести при условии, что каждая команда после игры на своем стадионе следующую проводит на "чужом" и наоборот - после игры на "чужом", следующая - на своем?
3. Докажите, что при любом натуральном n > 7 любой четырехугольник можно разрезать на n равнобедренных треугольников.
4. Назовем обрезком числа новое число, получаемое стиранием одной или нескольких последовательных начальных цифр данного числа. Найдите наибольшее пятизначное число, которое делится на все свои обрезки.
5. На поле a1 шахматной доски стоит ладья. Два игрока по очереди делают ходы ладьей, не ставя ее на поле, на которое она уже становилась. Выигрывает тот, кто первым поставит ладью на поле h8. Кто выиграет при правильной игре?
6. Кузнечик прыгает по прямой. Первый его прыжок на один см, второй на два см, ..., k-ый прыжок - на k см в ту или другую сторону. Он совершил 1998 прыжков. Мог ли он по ходу дела 500 раз вернуться в исходную точку?
7. В классе 12 девочек и 12 мальчиков, все - разного роста. На уроке физкультуры их построили в две шеренги (одна - позади другой): мальчиков - по росту слева направо, а девочек - по росту справа налево. Затем из каждой пары мальчик-девочка вызвали более высокого. Докажите, что вызвали двенадцать самых высоких учеников.
8. На катетах прямоугольного треугольника выбрали по точке. Докажите, что на соединяющем их отрезке есть точка, расстояние от которой до вершины прямого угла меньше, чем до каждого из концов гипотенузы.
1. Решите в натуральных числах уравнение (n!)2 + n! = m!
2. Внутри параллелограмма ABCD взяли точку O. Докажите, что OA<OB+OC+OD.
3. На шахматной доске отметили 17 клеток. Докажите, что среди них есть две такие, что с одной на другую конь может попасть не более чем за два хода.
4. Есть чашечные весы, кран и три одинаковых, достаточно вместительных сосуда без разметки. В один сосуд налито 7 л воды, в другой - 10 л, а третий пуст. Разрешается ставить два сосуда на весы и доливать в один из них воду (из крана или третьего сосуда), пока весы не уравновесятся. Можно также переливать всю воду из одного сосуда в другой и выливать воду из сосуда в раковину. Как отмерить 19 л воды в одном из сосудов?
5. Какое наименьшее значение может принимать НОК шести попарно различных натуральных чисел, если известно, что произведение любых двух из этих чисел делится на 2, любых трех - на 3, любых четырех - на 4, любых пяти - на 5?
6. Обозначим через A количество способов раскрасить прямоугольник 7*8 в восемь цветов так, чтобы в каждой строке и каждом столбце все цвета были различны, а через B - количество способов раскрасить по этим же правилам квадрат 8*8. Что больше: А или В?
7. Найти наибольшее число, кратное 27, в записи которого каждая цифра встречается не более одного раза.
8. Сколькими различными способами можно зашнуровать ботинок, чтобы
снаружи шнуровка выглядела так, как показано на рисунке справа?
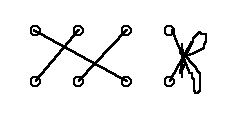
1. Прямоугольник двумя прямыми, параллельными одной паре сторон, и одной прямой, параллельной другой паре сторон, разделен на шесть прямоугольных частей. За один вопрос можно узнать площадь одной из частей. Как за четыре вопроса можно узнать площадь исходного прямоугольника?
2. Натуральные числа a и b, таковы, что (a - b)2 = НОК(a, b). Докажите, что НОД(a, b) > 1.
3. В классе 17 учеников. Известно, что среди любых трех учеников найдутся хотя бы два друга. Доказать, что в классе есть ученик, у которого не менее 8 друзей.
4. Существует ли натуральное число n, у которого сумма цифр такая же, как у числа n2 - 1?
5. На математическом конкурсе было предложено несколько простых и несколько сложных задач. Участнику давали 3 очка за решение сложной задачи и 2 очка - за решение простой задачи. Кроме того, за каждую нерешенную простую задачу снималось одно очко. Рома решил 10 задач и набрал 14 очков. Сколько простых задач было предложено на конкурсе?
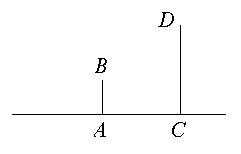
6. К прямой АС восставлены перпендикуляры AB и
CD, причем AB не равно CD. Назовем точку О
хорошей, если /AOB = /COD. Укажите на
плоскости три различные хорошие точки.
7. Есть пять монет достоинством 1, 2, 3, 5 и 10 ижиков. Четыре из них - настоящие, их вес в граммах равен их достоинству, а одна - фальшивая, ее вес в граммах не равен ее достоинству. Как, используя только чашечные весы без гирь, найти фальшивую монету?
8. Шахматный слон ходит по диагонали на любое число клеток. Назовем ход слона нечетным, если слон за этот ход переместился на нечетное число клеток. Однажды слон, сделав несколько ходов, попал из левого нижнего в правый верхний угол шахматной доски (8*8). Докажите, что он сделал нечетное число нечетных ходов.
1. В вершинах шестиугольника выписаны числа, а на каждой стороне - сумма чисел в ее концах. Назовем округлением замену нецелого числа на одно из двух ближайших целых (с недостатком или с избытком), а целое пусть при округлении не меняется. Докажите, что можно все 12 чисел округлить так, чтобы по-прежнему на каждом ребре стояла сумма чисел в его концах.
2. За столом сидят несколько мальчиков и 5 девочек, а на тарелке лежат 60 булочек. Каждая девочка дала по булочке (с тарелки) каждому знакомому ей мальчику, а каждый мальчик дал по булочке (с тарелки) каждой незнакомой ему девочке. После этого оказалось, что все булочки розданы. Сколько было мальчиков?
3. На всех черных клетках шахматной доски размером 4*4 стоит по коню. Сколькими различными способами они могут одновременно прыгнуть так, чтобы после прыжка все кони снова оказались на разных клетках?
4. Для игры в классики на земле нарисован ряд клеток, в которые вписаны по порядку числа от 1 до 10 (см. рис). Маша прыгнула снаружи в клетку 1, затем попрыгала по остальным клеткам (каждый прыжок - на соседнюю по стороне клетку) и выпрыгнула наружу из клетки 10. Известно, что на клетке 1 Маша была 1 раз, на клетке 2 - 2 раза, ..., на клетке 9 - 9 раз. Сколько раз побывала Маша на клетке 10?
| 1 | 4 | 5 | 8 | 9 |
| 2 | 3 | 6 | 7 | 10 |
5. В ряд были выписаны натуральные числа 1, 2, 3,...,n. Их стали записывать в новом порядке: сперва по возрастанию все кратные 2 (то есть 2, 4, 6,...), затем по возрастанию - оставшиеся, кратные 3 (то есть 3, 9, 15,...), далее - оставшиеся, кратные 5, потом - кратные 7 и т.д. В результате число 1997 снова оказалось на 1997-м месте. При каких n это возможно?
6. По кругу записаны 12 различных натуральных чисел. Известно, что для любых двух соседей отношение большего к меньшему - целое число. Могут ли все эти отношения быть меньше 20, но больше 10?
7. Сумма длин двух диагоналей выпуклого пятиугольника больше, чем сумма длин трех других диагоналей. Докажите, что эти две диагонали исходят из одной вершины.
8. В записи трех трехзначных чисел использованы только цифры 1, 8 и 9. Сумма этих чисел равна 1998. Докажите, что если в каждом из них поменять местами первую и последнюю цифры, то их сумма не изменится.
1. Имеются два бикфордовых шнура. Каждый горит ровно минуту, но, к сожалению, неравномерно. Можно ли с их помощью отмерить 45 секунд?
2. В однокруговом турнире по футболу участвует 18 команд, у каждой из которых имеется свой стадион. Какое наибольшее количество команд может провести все 17 туров при условии, что каждая команда после игры на своем стадионе следующую проводит на "чужом" и наоборот - после игры на "чужом", следующая - на своем?
3. Назовем обрезком числа новое число, получаемое стиранием одной или нескольких последовательных начальных цифр данного числа. Найдите наибольшее пятизначное число, которое делится на все свои обрезки.
4. На поле a1 шахматной доски стоит ладья. Два игрока по очереди делают ходы ладьей, не ставя ее на поле, на которое она уже становилась. Выигрывает тот, кто первым поставит ладью на поле h8. Кто выиграет при правильной игре?
5. Аня, Вера и Галя ели конфеты. Аня и Вера съели на 11 конфет больше Гали, а Аня и Галя - на 7 конфет больше Веры. Сколько конфет съела Аня?
6. Кузнечик прыгает по прямой. Первый его прыжок на один см, второй на два см, ..., k-ый прыжок - на k см в ту или другую сторону. Он совершил 1998 прыжков. Мог ли он по ходу дела 500 раз вернуться в исходную точку?
7. Назовем размером четырехугольника сумму длин всех его сторон и диагоналей. Можно ли в меньший по размеру выпуклый четырехугольник поместить больший?
8. В классе 12 девочек и 12 мальчиков, все - разного роста. На уроке физкультуры их построили в две шеренги (одна - позади другой): мальчиков - по росту слева направо, а девочек - по росту справа налево. Затем из каждой пары мальчик-девочка вызвали более высокого. Докажите, что вызвали двенадцать самых высоких.