10-й Математический Праздник.
21 февраля 1999 года

7 класс

1. [4 балла] Числитель и знаменатель дроби - целые положительные числа, дающие в сумме 101. Известно, что дробь не превосходит 1/3. Укажите наибольшее возможное значение такой дроби.

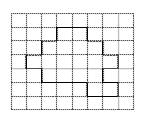
2. [4 балла] Разрежьте фигуру (по границам клеток) на три равные (одинаковые по форме и величине) части.

3. [4 балла] Из Москвы вылетел вертолёт, который пролетел 300 км на юг, потом 300 км на запад, 300 км на север и 300 км на восток, после чего приземлился. Оказался ли он южнее Москвы, севернее её или на той же широте? Оказался ли он восточнее Москвы, западнее Москвы или на той же долготе?

4. [6 баллов] Два пешехода вышли на рассвете. Каждый шёл с постоянной скоростью. Один шёл из A в B, другой - из B в A. Они встретились в полдень и, не прекращая движения, пришли: один в B в 4 часа вечера, а другой - в A в 9 часов вечера. В котором часу в тот день был рассвет?

5. [6 баллов] Нарисуйте на клетчатой бумаге треугольник с вершинами в углах клеток, две медианы которого перпендикулярны. (Медиана соединяет вершину треугольника с серединой противоположной стороны.)

6. [8 баллов] Квадрат разбили на 100 прямоугольников девятью вертикальными и девятью горизонтальными прямыми (параллельными его сторонам). Среди этих прямоугольников оказалось ровно 9 квадратов. Докажите, что два из этих квадратов имеют одинаковый размер.

Дата последнего изменения: 17 января 2000 года