|
||||||||||
8-й математический праздник.
16 февраля 1997 года
7 класс
1. Каких прямоугольников с целыми
сторонами больше: с периметром 1996 или с периметром 1998?
(Прямоугольники a x b и b x a считаются одинаковыми.)
(С.Дориченко)
2. В Мексике экологи добились принятия закона,
по которому каждый автомобиль хотя бы один день
в неделю не должен ездить (владелец сообщает полиции
номер автомобиля и "выходной" день недели
этого автомобиля). В некоторой семье все взрослые
желают ездить ежедневно (каждый - по своим делам!).
Сколько автомобилей должно быть в семье, если взрослых
в ней а) (2 балла) 5 человек? б) (3 балла) 8 человек?
(И.Ященко)
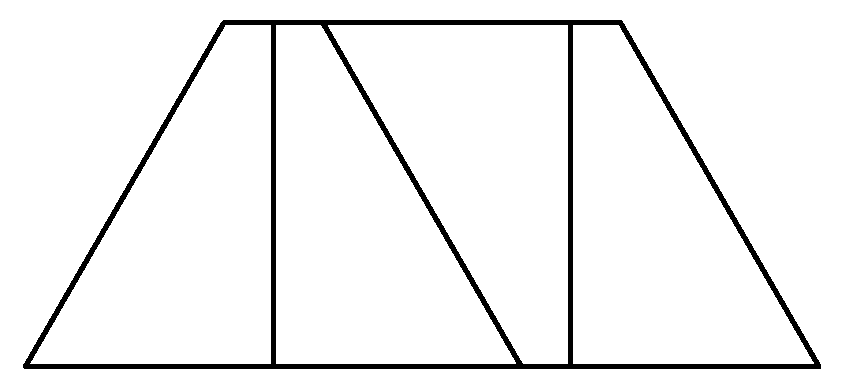 3 (5 баллов). Четырехугольник с
длинами сторон 1, 1, 1 и 2 имеет две параллельные стороны и
разбит на четыре одинаковые фигуры (см. рисунок). В результате
верхняя сторона разделилась на четыре отрезка. Найти отношение
длины большего отрезка к меньшему.
3 (5 баллов). Четырехугольник с
длинами сторон 1, 1, 1 и 2 имеет две параллельные стороны и
разбит на четыре одинаковые фигуры (см. рисунок). В результате
верхняя сторона разделилась на четыре отрезка. Найти отношение
длины большего отрезка к меньшему.
(А.Ковальджи)
4 (5 баллов). В корзине лежат 30 грибов.
Известно, что среди любых 12 грибов имеется хотя бы
один рыжик, а среди любых 20 грибов - хотя бы один
груздь. Сколько рыжиков и сколько груздей в корзине?
(А.Галочкин)
5 (6 баллов). В тесте к каждому вопросу указаны 5 вариантов ответа.
Отличник отвечает на все вопросы правильно.
Когда двоечнику удается списать, он отвечает правильно, а в
противном случае - наугад (то есть среди несписанных вопросов
он правильно отвечает на 1/5 часть). За год двоечник правильно
ответил на половину вопросов. Какую долю ответов ему удалось
списать?
(А.Спивак, И.Ященко)
6.
Если смотреть на аквариум
спереди, то рыбка проплыла, как показано на левом рисунке.
А если справа - то как на правом рисунке. Нарисовать вид сверху.
(А.Шень)
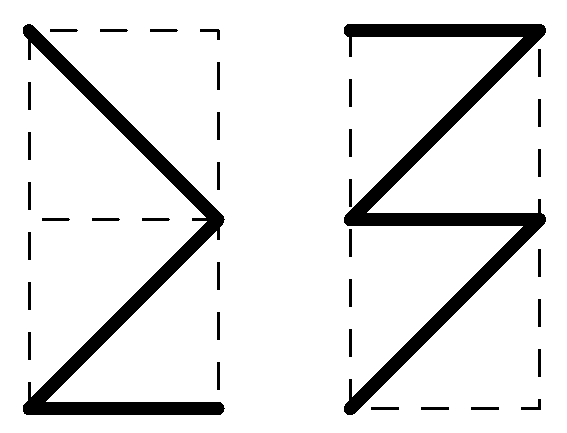
Дата последнего изменения: 17 января 2000 года







