11-й Математический Праздник.
13 февраля 2000 года

Условия задач.

7 класс

Задача 1. [3 балла]
В квадрате 7*7 клеток закрасьте некоторые клетки так, чтобы в каждой строке и в каждом столбце оказалось ровно по 3 закрашенных клетки. [3 балла]

Задача 2.
Карлсон написал дробь 10/97. Малыш может:
1) прибавлять любое натуральное число к числителю и знаменателю одновременно,
2) умножать числитель и знаменатель на одно и то же натуральное число.
Сможет ли Малыш с помощью этих действий получить дробь,
а) равную 1/2? [2 балла]
б) равную 1? [4 балла]

Задача 3.
Дан прямоугольный треугольник. Приложите к нему какой-нибудь треугольник (эти треугольники должны иметь общую сторону, но не должны перекрываться даже частично) так, чтобы получился треугольник с двумя равными сторонами.

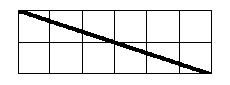
Укажите (нарисуйте!) несколько различных решений.
Каждое новое решение - [1 балл].

Задача 4. [8 баллов]
Может ли произведение двух последовательных натуральных чисел равняться произведению двух последовательных чётных чисел?

Задача 5. [10 баллов]
В вершинах куба ABCDEFGH расставлены натуральные числа так, что числа в соседних (по ребру) вершинах отличаются не более чем на единицу. Докажите, что обязательно найдутся две диаметрально противоположные вершины, числа в которых отличаются не более чем на единицу.

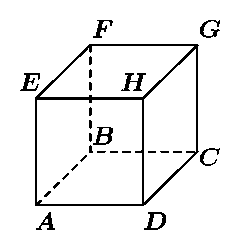
(Пары диаметрально противоположных вершин куба: A и G, B и H, C и E, D и F.)

Авторы задач:
А. Ю. Митягин (1), В. В. Клепцын (2), А. Шень (3), В. В. Произволов (4), Г. А. Гальперин (5)

Дата последнего изменения: 15 февраля 2000 года