9-й математический праздник.
22 февраля 1998 года

6 класс

1. (4 балла) На глобусе проведены 17 параллелей и 24 меридиана. На сколько частей разделена поверхность глобуса? Меридиан - это дуга, соединяющая Северный полюс с Южным. Параллель - это окружность, параллельная экватору (экватор тоже является параллелью).
(М.Семенова)

2. (4 балла) Три ежика не могли поделить поровну три кусочка сыра массами 5г, 8г и 11г. Лиса стала им помогать. Ей разрешили от любых двух кусочков отрезать по 1г сыра (обрезки лиса съедает). Сможет ли лиса оставить ежикам равные кусочки сыра?
(А.Ковальджи)

3. (8 баллов) Расположите в кружочках (вершинах правильного десятиугольника) числа от 1 до 10 так, чтобы для любых двух соседних чисел их сумма была равна сумме двух чисел, им противоположных (симметричных относительно центра окружности).
(фольклор)

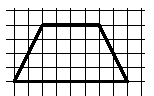4. (8 баллов) Разрежьте фигуру, изображенную на рисунке, на две части, из которых можно сложить треугольник.
(фольклор)

5. На кольцевой дороге расположены четыре бензоколонки: A, B, C и D. Расстояние между A и B - 50 км, между A и C - 40 км, между C и D - 25 км, между D и A - 35 км (все расстояния измеряются вдоль кольцевой дороги в кратчайшую сторону).
а) (4 балла) Приведите пример расположения бензоколонок (с указанием расстояний между ними), удовлетворяющий условию задачи.
б) (8 баллов) Найдите расстояние между B и C (укажите все возможности).
(И.Ященко)

6. (16 баллов) Расставьте на шахматной доске 32-х коней так, чтобы каждый из них бил ровно 2-х других.
(М.Евдокимов)

Дата последнего изменения: 17 января 2000 года