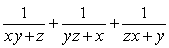Командная олимпиада
1. Точки E, F, K, M - соответственно середины отрезков AB, CD, AD, AK в выпуклом четырехугольнике ABCD, прямые AF, CM, BK, DE пересекаются в одной точке О. Докажите, что площадь четырехугольника BOFC равна половине площади четырехугольника ABCD.
2. Даны два квадратных уравнения вида аx2+bx+c=0. Рассматриваются всевозможные уравнения, которые получаются, если к первому несколько раз прибавить второе. Среди них оказалось бесконечно много уравнений, имеющих хотя бы один целый корень. Докажите, что исходные уравнения имеют общий целый корень.
3. Пусть n - некоторое натуральное число. Имеется n бесконечных арифметических прогрессий из натуральных чисел, таких, что никакое число из второй сотни (101, 102, ... , 200) не принадлежит ни одной из этих прогрессий, а любое другое натуральное число содержится хотя бы в одной из них. При каком наименьшем n это возможно?
4. В куче лежит n спичек. Двое играющих берут по очереди от одной до десяти спичек за ход. Взявший последнюю спичку получает премиальный коробок с 60 спичками. Выигрывает тот, у кого с учетом премии в сумме окажется больше спичек. Докажите, что при достаточно большом значении n начинающий игрок может играть так, чтобы не проиграть, независимо от ходов соперника.
5. Квадрат 6*6 разбивают на прямоугольники 1*2. Какое наибольшее количество пар соседних (то есть имеющих общий отрезок границы) прямоугольников может при этом получиться?
6. Для каждой последовательности длины 1997, составленной из чисел 1 и -1,
вычислили квадрат суммы входящих в нее чисел. Найдите среднее арифметическое
всех таких квадратов.
1. Найдите хотя бы одно натуральное число, сумма всех делителей которого
(исключая само это число) равна 1997.
2. Квадратный ящик со стороной 10 разбит на квадратные ячейки со стороной 1,
в каждой из которых лежит по шару. Внешне все шары одинаковы, но ровно один из
них радиоактивен. Имеется детектор, которым можно накрыть любые четыре ячейки,
образующие квадрат 2*2, и он покажет, имеется ли в этих ячейках радиоактивный
шар. Можно ли за 24 проверки наверняка найти этот шар?
3. За круглым столом сидят 12 человек, некоторые из которых всегда говорят
только правду (назовем их рыцарями), а остальные всегда лгут (назовем их
лжецами). Каждый из сидящих за столом произнес: "Напрротив меня сидит лжец".
Сколько всего лжецов сидит за столом?
4. Даны положительные числа a, b и с такие, что
a2=11, b2=13, c2=48.
Верно ли, что a+b=c?
5. Пусть M - точка пересечения медиан треугольника ABC.
Известно, что вписанные в треугольники ABM, BCM и CAM
круги равны и попарно касаются друг друга. Докажите, что треугольник ABC
равносторонний.
6. Пусть N - число способов разбиения квадрата на прямоугольники 2*1.
Докажите, что N делится на 2.
1. Пусть M - точка пересечения медиан треугольника ABC.
Известно, что вписанные в треугольники ABM, BCM и CAM
круги равны и попарно касаются друг друга. Докажите, что треугольник ABC
равносторонний.
2. Пусть N - число способов разбиения куба на прямоугольные
параллелепипеды 2*1*1. Докажите, что N делится на 3.
3. Даны числа a2, b2,
c2 (a, b и с - положительные числа).
Разрешается выполнять операции сложения, вычитания и умножения, а также
запоминать любое количество промежуточных результатов и сравнивать их между
собой. Можно ли, используя только эти операции, проверить справедливость
равенства a+b=c?
4. Квадратный ящик со стороной 1997 разбит на квадратные ячейки со стороной
1, в каждой из которых лежит по шару. Внешне все шары одинаковы, но ровно один
из них радиоактивен. Имеется детектор, которым можно накрыть любые четыре
ячейки, образующие квадрат 2*2, и он покажет, имеется ли в этих ячейках
радиоактивный шар. За какое наименьшее число таких проверок можно наверняка
найти этот шар?
5. В треугольнике ABC на стороне AC существует единственная
точка D, такая, что BD2=AD*CD. Докажите,
что BD - биссектриса угла ABC.
6. Докажите, что для любых положительных a и b выполняется
неравенство
1. Пусть M - точка пересечения медиан треугольника ABC.
Известно, что вписанные в треугольники ABM, BCM и CAM
круги равны и попарно касаются друг друга. Докажите, что треугольник
ABC равносторонний.
2. Пусть N - число способов разбиения куба на прямоугольные
параллелепипеды 2*1*1. Докажите, что N делится на 3.
3. Квадратный ящик со стороной 1997 разбит на квадратные ячейки со стороной
1, в каждой из которых лежит по шару. Внешне все шары одинаковы, но ровно один
из них радиоактивен. Имеется детектор, которым можно накрыть любые четыре
ячейки, образующие квадрат 2*2, и он покажет, имеется ли в этих ячейках
радиоактивный шар. За какое наименьшее число таких проверок можно наверняка
найти этот шар?
4. В треугольнике ABC на стороне AC существует единственная
точка D, такая, что BD2=AD*CD.
Докажите, что BD - биссектриса угла ABC.
5. Докажите, что для любых положительных a и b выполняется
неравенство
6. Можно ли расставить натуральные числа в клетках шахматной доски так,
чтобы в каждой паре соседних (имеющих хотя бы одну общую вершину) клеток одно
из чисел делилось на другое, а для каждой пары несоседних клеток такого не было?
1. Можно ли в тригонометрическом уравнении
2. Отрезок разбит на конечное число отрезков, некоторые из которых
покрашены в синий цвет, а остальные - в красный (концы отрезков не покрашены).
Известно, что совокупность всех красных отрезков можно так наложить на
совокупность всех синих отрезков (не сдвигая одноцветные отрезки друг
относительно друга), что эти совокупности совместятся. Докажите, что к центру
исходного отрезка с одной стороны примыкает синий отрезок, а с другой -
красный.
3. Квадратный ящик со стороной 1997 разбит на квадратные ячейки со стороной
1, в каждой из которых лежит по шару. Внешне все шары одинаковы, но ровно один
из них радиоактивен. Имеется детектор, которым можно накрыть любые четыре
ячейки, образующие квадрат 2*2, и он покажет, имеется ли в этих ячейках
радиоактивный шар. За какое наименьшее число таких проверок можно наверняка
найти этот шар?
4. В треугольнике ABC на стороне AC существует единственная
точка D, такая, что BD2=AD*CD.
Докажите, что BD - биссектриса угла ABC.
5. Можно ли расставить натуральные числа в клетках шахматной доски так,
чтобы в каждой паре соседних (имеющих хотя бы одну общую вершину) клеток одно
из чисел делилось на другое, а для каждой пары несоседних клеток такого не было?
6. Найдите все положительные значения k, при которых неравенство
1. Пусть а1, а2, ... - все натуральные
делители числа а, расположенные в порядке возрастания,
b1, b2, ... - все натуральные делители
числа b, расположенные в порядке возрастания. Известно, что
аn+bn=a,
an+1+bn+1=b.
Найдите числа a и b (в зависимости от n).
2. Страна Квадрандия квадратна и разбита на нечетное число прямоугольных
княжеств. Барон Мюнхгаузен утверждает, что он смог совершить путешествие по
Квадрандии, пройдя каждое княжество ровно один раз по диагонали, и вернуться
в исходную точку, ни в какой другой точке не побывав дважды. Не хвастает ли
барон?
3. О функции f: R-->R известно, что множество
значений суммы f(x)+f(2x) конечно.
Обязательно ли множество значений f(x) конечно?
4. Докажите, что для любых положительных a и b выполняется
неравенство:
5. В пятиугольник вписана окружность. Каждую вершину соединили с точкой
касания окружности с противоположной стороной пятиугольника. Четыре из пяти
проведенных отрезков прошли через одну точку. Докажите, что через нее проходит
и пятый отрезок.
6. Существуют ли 1997 попарно различных натуральных чисел, являющихся
полными квадратами, чья десятичная запись отличается друг от друга лишь
перестановкой цифр?
7. Докажите, что количество способов разбить доску 8*8 на прямоугольники
1*2 не превосходит 230.
8. Найдите все натуральные числа N, не меньшие трех, для каждого из
которых существует множество из N различных натуральных чисел,
обладающее следующим свойством: для любого числа A из этого множества
найдутся два отличных от него и друг от друга числа B и C из
этого же множества, такие, что A=B+C или
A=(B+C)/5.
9. Есть n точек на плоскости, никакие три из которых не лежат на
одной прямой. При каком наибольшем n можно наверняка разбить плоскость
на части 1997-ю прямыми, не проходящими через эти точки, так, чтобы все n
точек оказались в разных частях?
10. Вася заменяет звездочки в выражении
1. Пусть а1, а2, ... - все натуральные
делители числа а, расположенные в порядке возрастания,
b1, b2, ... - все натуральные делители
числа b, расположенные в порядке возрастания. Известно, что
а10+b10=a,
a11+b11=b. Найдите числа а
и b.
2. Страна Квадрандия квадратна и разбита на нечетное число прямоугольных
княжеств. Некто совершил путешествие по Квадрандии, начав из одного ее угла,
пройдя каждое княжество ровно один раз по диагонали и завершив путешествие в
другом углу. Услышав об этом, барон Мюнхгаузен пообещал совершить аналогичное
путешествие, начало и конец которого будут находиться в двух других углах.
Всегда ли барон сможет выполнить это свое обещание?
3. О последовательности an известно, что множество
значений сумм an+a2n и
an+a4n конечно. Обязательно ли
множество значений an конечно?
4. Существуют ли 1997 попарно различных натуральных чисел, являющихся
полными квадратами, чья десятичная запись отличается друг от друга лишь
перестановкой цифр?
5. Пятиугольник вписан в окружность. Известно, что касательные к окружности,
проведенные в некоторых четырех вершинах пятиугольника, соответственно
параллельны его противолежащим сторонам. Докажите, что этот пятиугольник
правильный (то есть в нем все углы равны между собой и все стороны также равны
между собой).
6. Последовательность чисел определена следующим образом:
a1=1997,
an+1=19an+96 для любого натурального
n. Могут ли какие-либо шесть ее последовательных членов оказаться
простыми числами?
7. Докажите, что количество способов разбить доску 8*8 на прямоугольники 1*2
не превосходит 231.
8. Найдите все натуральные числа N, не меньшие трех, для каждого из
которых существует множество из N различных натуральных чисел,
обладающее следующим свойством: для любого числа A из этого множества
найдутся два отличных от него и друг от друга числа B и C из
этого же множества, такие, что A=B+C или
A=(B+C)/5.
9. Есть n точек на плоскости, никакие три из которых не лежат на
одной прямой. При каком наибольшем n можно наверняка разбить плоскость
на части тремя прямыми, не проходящими через эти точки, так, чтобы все
n точек оказались в разных частях?
10. Вася заменяет звездочки в выражении
1. Единичный квадрат разбит на 1012 квадратиков. Может ли сумма
периметров квадратиков, имеющих хотя бы одну общую точку с фиксированной
диагональю единичного квадрата, быть больше 100?
2. На координатной плоскости нарисовали три параболы - графики квадратных
трехчленов. Оказалось, что множество точек, лежащих более чем на одной параболе,
совпадает со множеством вершин парабол. Докажите, что найдутся две параболы,
имеющие ровно одну общую точку.
3. Существует ли натуральное число, которое не является делителем никакого
натурального числа с суммой цифр, меньшей 1997?
4. Положительные числа
a1, a2, ..., an,...
образуют бесконечно возрастающую геометрическую прогрессию. Может ли
последовательность дробных частей этих чисел оказаться бесконечно убывающей
геометрической прогрессией?
5. Все натуральные числа выписали подряд: 1234567891011... . Для каждого
натурального числа вычислили произведение всех ненулевых цифр, стоящих в этом
ряду слева от него (например, для числа 13 получилось произведение
1*2*3*4*5*6*7*8*9*1*1*1*1*2 = 725760). Верно ли, что среди получившихся
произведений бесконечно много точных 1997-х степеней?
6. Существует ли числовая функция f(x), определенная на
отрезке [-2;4] и принимающая все свои значения на том же отрезке, которая при
всех x 7. Рассмотрим произведение десяти попарно различных натуральных сомножителей,
каждый из которых не больше 30 и никакие два из которых не различаются ровно на
10 или ровно на 20. Найдите сумму всевозможных таких произведений.
8. Докажите, что указанную на рисунке фигуру (составленную из квадратиков)
нельзя разрезать по линиям сетки на два одинаковых многоугольника.
9. Пусть Х - непустое конечное множество. Двое по очереди называют
непустые подмножества множества Х, причем запрещается называть такие,
которые содержат хотя бы одно уже названное подмножество. Проигрывает тот
игрок, который не может сделать очередной ход. Кто выигрывает при правильной
игре?
10. H - основание высоты AH остроугольного треугольника
АВС, М - середина стороны АВ. Докажите, что прямая
МН пересекает вписанную окружность треугольника АВС.
1. Кузнечик совершил три прыжка по плоскости. Его первый прыжок - на
1 м, второй - на 2 м, третий - на 4 м. Найдите фигуру,
образованную всеми точками плоскости, до которых кузнечик сможет, начиная с
данной точки, допрыгать за три описанных прыжка.
2. На координатной плоскости нарисовали три параболы - графики квадратных
трехчленов. Оказалось, что множество точек, лежащих более чем на одной параболе,
совпадает со множеством вершин парабол. Докажите, что найдутся две параболы,
имеющие ровно одну общую точку.
3. Среднюю школу села Ерши окончили 10 юношей и 10 девушек. На выпускном
вечере каждый юноша поссорился с 17 одноклассниками, а каждая девушка - с 9
одноклассниками. Докажите, что последний танец могли танцевать одновременно не
меньше пяти пар не ссорившихся между собой юношей и девушек.
4. Назовем диагональ выпуклого семиугольника малой, если она
соединяет концы соседних его сторон. Докажите, что всегда можно построить
выпуклый семиугольник, стороны которого равны и параллельны малым диагоналям
данного выпуклого семиугольника.
5. Можно ли расставить в вершинах и на ребрах куба натуральные числа так,
чтобы на каждом ребре стоял НОД чисел в его концах, и на ребрах встретились
все числа от 1 до 12?
6. В одной двухлитровой банке - 96 мл воды, во второй - 160 мл,
в третьей - 896 мл. Разрешается перелить из любой банки в любую другую
столько воды, сколько в этой другой уже есть. Можно ли такими операциями
собрать всю воду в одном сосуде?
7. Рассмотрим произведение десяти попарно различных натуральных сомножителей,
каждый из которых не больше 20 и никакие два из которых не различаются ровно на
10. Найдите сумму всевозможных таких произведений.
8. Докажите, что указанную на рисунке фигуру (составленную из квадратиков)
нельзя разрезать по линиям сетки на два одинаковых многоугольника.
9. Пусть Х - непустое конечное множество. Двое по очереди называют
непустые подмножества множества Х, причем запрещается называть такие,
которые содержат хотя бы одно уже названное подмножество. Проигрывает тот игрок,
который не может сделать очередной ход. Кто выигрывает при правильной игре?
10. H - основание высоты AH остроугольного треугольника
АВС, М - середина стороны АВ. Докажите, что прямая
МН пересекает вписанную окружность треугольника АВС.
1. В ста ящиках находятся спички: в первом - одна, во втором - две, ...,
в сотом - сто. Двое игроков по очереди берут по две спички, каждый раз - из
двух различных ящиков. Проигрывает тот, кто не может сделать очередной ход.
Кто выигрывает при правильной игре и как он для этого должен играть?
2. На боковых сторонах АВ и ВС равнобедренного треугольника
АВС отметили точки М и N соответственно. На стороне
АС отметили точкиL и K, отличные от вершин треугольника.
Оказалось, что BM=BN=AL=LK=KC=1 и лучи
LB и KB - биссектрисы углов MLN и MKN
соответственно. Найдите длины сторон треугольника АВС.
3. Обозначим через Mn множество всех целочисленных пар
(x;y), удовлетворяющих уравнению
x2+xy+2y2=n. Докажите, что
4. Для произвольного треугольника ABC и для произвольной тройки чисел (x; y; z) назовем их согласованностью количество различных точек M плоскости треугольника ABC, таких, что тройка расстояний (MA; MB; MC) является перестановкой тройки (x; y; z). Какие значения может принимать эта величина?
5. Секретный объект представляет собой в плане квадрат 8*8, разбитый
коридорами на квадратики 1*1. В каждой вершине такого квадратика - выключатель.
Щелчок выключателя действует сразу на все выходящие из этой вершины метровые
коридоры, меняя их освещенности на противоположные. Сторож находится в углу
полностью неосвещенного объекта. Он может ходить только по освещенным
коридорам и щелкать выключателями любое число раз. Может ли сторож добиться
того, чтобы от любого выключателя к любому другому он мог пройти, не щелкая
выключателями?
6. Какое наибольшее число диагоналей можно провести в выпуклом
n-угольнике так, чтобы каждая из них пересекалась внутри
n-угольника не более, чем с одной другой?
7. Паук соединил связной паутиной все восемь углов комнаты 3*3*3. Может ли
общая длина паутины быть меньше 19?
8. Квадратный трехчлен
f(x)=ах2+bx+c с целыми коэффициентами
обладает таким свойством: для любого натурального m найдется
натуральное х такое, что f(x) делится на m.
Докажите, что корни f(x) рациональны.
9. На встречу глав государств прибыли N > 4 президентов,
каждый из которых знает только один язык. Организаторы встречи так обучили
N переводчиков, что каждый из них знает три языка и при любой рассадке
президентов за круглым столом можно так рассадить переводчиков между ними,
чтобы все президенты смогли общаться со своими ближайшими соседями через
сидящего между ними переводчика. Сколько президентов могло быть на встрече?
10. Докажите, что всякое натуральное число может быть представлено в виде отношения двух натуральных чисел, в записи каждого из которых встречаются подряд цифры 1997.
1. Пять прямых, являющихся графиками функций
y=aix+bi
(1<i<5), где не все bi одинаковы,
имеют общую точку. Докажите, что пять прямых
y=bix+ai также имеют общую точку.
2. В поход собрались туристы и инструкторы (конечно же, туристов больше).
Каждый турист взял с собой по пять лыжных палок и совсем не брал рукавиц, а
каждый инструктор взял лишь по две лыжных палки, но зато также взял по семь
рукавиц. Оказалось, что общее количество лыжных палок на столько же превосходит
общее количество рукавиц, на сколько процентов туристов больше, чем
инструкторов. Сколько инструкторов собралось в поход?
3. По кругу в некотором порядке выписали все натуральные числа от 1 до 1000,
каждое - ровно один раз. Одновременно для каждого числа подсчитали сумму трех
следующих за ним по ходу часовой стрелки и результат записали вместо исходного
числа. Может ли оказаться, что все получившиеся числа, кроме не более чем
десяти из них, кратны 5?
4. Для какого наименьшего n > 1 можно разрезать квадрат ровно на
n попарно различных подобных прямоугольников?
5. На боковых сторонах АВ и ВС равнобедренного треугольника
АВС отметили точки М и N соответственно. На стороне
АС отметили точкиL и K, отличные от вершин треугольника.
Оказалось, что BM=BN=AL=LK=KC=1 и лучи
LB и KB - биссектрисы углов MLN и MKN
соответственно. Найдите длины сторон треугольника АВС.
6. Над строкой чисел можно производить следующие операции: стереть все
числа, стоящие на четных местах, или стереть все числа, стоящие на нечетных
местах (после каждой такой операции места нумеруются заново). Над строкой 1,
2, ..., 1997 последовательно выполняют эти операции до тех пор, пока не
останется ровно два числа. Могут ли они оба делиться на 13?
7. В Зурбагане сеть железных дорог устроена следующим образом: все города
стоят на кольце, кроме того, столица соединена отдельными ветками с каждым из
городов, кроме соседей по кольцу. Правительство Зурбагана разбило сеть на
участки между соседними городами и постановило разделить эти участки между
двумя компаниями так, чтобы можно было проехать между любыми двумя городами как
по дорогам только первой компании, так и по дорогам только второй компании.
Может ли это постановление быть выполнено?
8. В ста ящиках находятся спички: в первом - одна, во втором - две, ...,
в сотом - сто. Двое игроков по очереди берут по две спички, каждый раз - из
двух различных ящиков. Проигрывает тот, кто не может сделать очередной ход.
Кто выигрывает при правильной игре и как он для этого должен играть?
9. Можно ли равносторонний треугольник со стороной 9 см разрезать на два
треугольника, периметры которых равны 20см и 23см?
Олимпиада, 8 класс
Олимпиада, 9 класс
(1/(a+b))+(1/a)+(1/b) > (5/2)/(ab)1/2
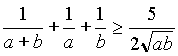 .
.
Олимпиада, 10 класс
(1/(a+b))+(1/a)+(1/b) > (5/2)/(ab)1/2
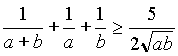
Олимпиада, 11 класс
a1cos x + a2sin 2x + a3cos 3x + a4sin 4x + ... + a1997cos 1997x = 0
так заменить коэффициенты действительными числами, чтобы полученное уравнение не
имело действительных корней?
(1/(a+b))+k((1/a)+(1/b)) > (4k+1)/(2(ab)1/2)
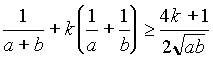
выполняется для любых положительных a и b.
Первый тур. Лига A
(((a2+2)1/2-1)/b) + (((b2+2)1/2-1)/a) > 21/2
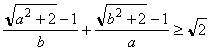
КВКОРЕНЬ(*КВКОРЕНЬ(... *КВКОРЕНЬ(*)...)
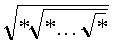 , содержащем n звездочек, числами
21, 22, ..., 2n, используя каждое ровно
один раз. Какое наибольшее целое число он может при этом получить?
, содержащем n звездочек, числами
21, 22, ..., 2n, используя каждое ровно
один раз. Какое наибольшее целое число он может при этом получить?
Первый тур. Лига B
(*/2) + (*/4) + ... + (*/2n)
числами 1, 2, ..., n, используя каждое ровно один раз. Какое наибольшее
целое число он может при этом получить?
Второй тур. Лига A
C[-2;4] удовлетворяет равенству
f(f(f(x))) = -x/2 и графиком которой
является ломаная, состоящая из конечного числа звеньев?
Второй тур. Лига B
Третий тур. Лига A
S(x;y)CMn(2xy+y2)=0
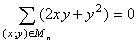 .
.
Третий тур. Лига B