Математическая регата 10 классов 15.04.2000
Задания | Результаты | План мероприятий Турнира Архимеда на 1999/2000 уч. г.
Задания
Первый тур (10 минут; каждая задача - 6 баллов).
1.1. Может ли график функции y=(ax2+bx+c)/(kx+l) иметь
следующий вид (см. рис.)?
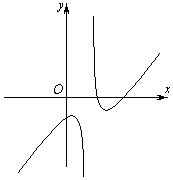
1.2. В равнобокую трапецию вписан круг радиуса r. Найдите длину
боковой стороны трапеции, если угол между диагональю и большим основанием равен
a
.
1.3. Квадрат 4*4 разрезают по границам клеток на четыре одинаковых
многоугольника. Сколькими способами это можно сделать (способы считаются
различными, если при разрезании получаются неравные многоугольники)?
Второй тур (15 минут; каждая задача - 7 баллов).
2.1. Может ли сумма возрастающей и убывающей функций быть
периодической функцией, отличной от постоянной?
2.2. Дан квадрат ABCD. На сторонах BC и CD выбраны точки K и N, так
что BK = KC и CN:ND = 2:1. Отрезки AK и BN пересекаются в точке T. Площадь
четырехугольника KCNT равна 13. Найдите площадь треугольника BTA.
2.3. Решите уравнение: 5cos5x + 3sin3x = 5.
Третий тур (15 минут; каждая задача - 7 баллов).
3.1. Решите систему уравнений:
| { | x/y = y/z = z/u = u/s = s/t; |
| x = 8u; |
| x + y + z + u + s + t = 15+(3/4) |
3.2. Существует ли тетраэдр, периметр каждой грани которого больше
суммы остальных трех ребер?
3.3. Какое наибольшее количество натуральных чисел, меньших
пятидесяти, надо взять, чтобы любые два из них были взаимно простыми?
Четвертый тур (20 минут; каждая задача - 8 баллов).
4.1. Решите уравнение:
1 + x2 + x4 + ... + x3998 +
x4000 = 2001x2000.
4.2. На сторонах треугольника ABC во внешнюю сторону построены
квадраты ABMP и BCDK. Докажите, что продолжение медианы BE треугольника ABC
является высотой треугольника BMK.
4.3. Решите уравнение в натуральных числах:
12x2 - 4x - 2xy + 3y - 9 = 0.
Пятый тур (25 минут; каждая задача - 9 баллов).
5.1. Существует ли натуральное n, такое что:
sin(21/2) + sin(2*21/2) + ...
+ sin(n*21/2) > 2000 ?
5.2. Существует ли такой пятиугольник, отличный от правильного, что
точки попарного пересечения его диагоналей являются вершинами пятиугольника,
который ему подобен?
5.3. Решите уравнение:
(x2 + [x] + 1)2 + [x2 + [x] + 1] = x - 1.
Результаты
Команда
школы | I | II | III | IV | V | Сумма
баллов | Место |
| 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 |
| 2А | 3 | 6 | 5 | 2 | 0 | 1 | 7 | 7 | 5 | 0 | 0 | 1 | 1 | 0 | 0 | 38 | 6 |
| 2Б | 4 | 6 | 4 | 7 | 3 | 0 | 7 | 7 | 6 | 1 | 0 | 0 | 1 | 0 | 9 | 55 | II |
| 7 | 0 | 3 | 6 | 0 | 0 | 0 | 5 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 15 | 16-17 |
| 109 | 6 | 0 | 6 | 2 | 0 | 0 | 0 | 0 | 4 | 3 | 0 | 0 | 0 | 0 | 0 | 21 | 12 |
| 152 | 6 | 1 | 6 | 0 | 2 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 17 | 14-15 |
| 218 | 6 | 0 | 5 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 2 | 1 | 0 | 9 | 26 | 11 |
| 548 | 0 | 0 | 6 | 0 | 1 | 1 | 7 | 7 | 2 | 0 | 0 | 0 | 1 | 0 | 6 | 31 | 9 |
| 1189А | 0 | 0 | 3 | 7 | 0 | 1 | 7 | 7 | 7 | 1 | 8 | 6 | 1 | 0 | 6 | 54 | III |
| 1189Б | 6 | 0 | 4 | 0 | 0 | 0 | 0 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 17 | 14-15 |
| 1511А | 1 | 0 | 6 | 7 | 0 | 1 | 2 | 0 | 4 | 0 | 0 | 0 | 1 | 0 | 6 | 28 | 10 |
| 1511Б | 5 | 0 | 6 | 7 | 0 | 1 | 1 | 7 | 3 | 0 | 0 | 1 | 1 | 5 | 0 | 37 | 7-8 |
| 1514А | 0 | 0 | 6 | 7 | 0 | 0 | 1 | 7 | 5 | 8 | 0 | 1 | 1 | 0 | 6 | 42 | V |
| 1514Б | 0 | 0 | 6 | 7 | 0 | 0 | 7 | 7 | 3 | 1 | 0 | 4 | 0 | 2 | 0 | 37 | 7-8 |
| 1534 | 6 | 6 | 5 | 7 | 0 | 0 | 4 | 7 | 5 | 0 | 0 | 8 | 1 | 0 | 0 | 49 | IV |
| 1543 | 0 | 2 | 6 | 7 | 3 | 7 | 0 | 7 | 7 | 0 | 8 | 0 | 1 | 0 | 9 | 57 | I |
| 1560А | 0 | 0 | 6 | 0 | 0 | 1 | 0 | 7 | 4 | 1 | 0 | 0 | 0 | 0 | 0 | 19 | 13 |
| 1560Б | 0 | 1 | 4 | 0 | 0 | 0 | 0 | 7 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 15 | 16-17 |