Введение в линейное программирование. 2
Введение в линейное программирование. 2
Оптимизация на графах с помощью линейного программирования
Моделирование в задаче про фермера
Баскетбольная задача: состав команды
Почтовому отделению требуется различное количество служащих в разные дни недели. Каждый сотрудник работает 5 дней подряд и затем два дня отдыхает.
Минимизируйте количество служащих, которых нужно нанять.
* День 1 (понедельник): требуется 17 служащих
* День 2 : требуется 13 служащих
* День 3 : требуется 15 служащих
* День 4 : требуется 19 служащих
* День 5 : требуется 14 служащих
* День 6 : требуется 16 служащих
* День 7 (воскресенье) : требуется 11 служащих
Жёсткие и мягкие ограничения
Фермер: жёсткие и мягкие ограничения
Задачу линейного программирования можно записать так, чтобы все нетривиальные условия были равенствами.
Для этого может потребоваться ввести новые переменные:
Площадь поля: x + y <= 75
Пусть s - площадь свободной (незасеянной) части поля
Площадь поля: x + y + s = 75
s >= 0
Подходы к ограничениям:
* запрет
* штраф
Что означает штраф:
* можно превысить доступные
площадь поля, объём склада, бюджет --- но за это придётся заплатить
Задача
Сформулируйте задачу про фермера на языке штрафов.
Оптимизация на графах с помощью линейного программирования
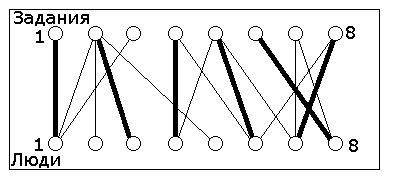
Список возможных заданий для каждого человека указан на рисунке.

Задача 1 Разминка: максимальное паросочетание
Каждый человек может одновременно делать одно задание.
Каждым заданием может заниматься один человек.
Найдите разбиение на пары (человек - задание), максимальное по числу пар.
Сформулируйте и решите как задачу линейного программирования.
Задача 2 Комбинируем доход
Каждому человеку можно поручить не более двух заданий.
Каждым заданием может заниматься один человек.
* Каждая пара (человек - задание) увеличивает доход на 1 руб.
Распределите задания, чтобы был максимальный доход.
* Каждое начатое дело увеличивает доход на 1 руб.
Распределите задания, чтобы был максимальный доход.
* Каждый занятый работник увеличивает доход на 1 руб.
Распределите задания (человек - задание), чтобы был максимальный доход.
* А теперь всё вместе:
Каждая пара (человек - задание) увеличивает доход на 1 руб.
Каждый бездельник (кто ничем не занят) уменьшает доход на 1 руб.
Каждое неначатое дело уменьшает доход на 1 руб.
Распределите задания, чтобы был максимальный доход.
Задача 3 От ограничений к штрафам
* Каждым заданием может заниматься один человек.
* Каждый человек охотно делает одно дело.
Если человек занят двумя делами, Вас штрафуют на 0.5 руб.
Если человек занят тремя делами, Вас штрафуют на 1 руб.
Каждая пара (человек - задание) увеличивает доход на 1 руб.
Распределите задания, чтобы был максимальный доход.
Приведите пример графа, когда штраф меняет
оптимальное распределение заданий.
При какой величине штрафа он превращается в запрет?
Задача 4 Штраф за модуль разности.
Две машины развозят покупателям 36 газовых плит.
За доставку каждой плиты Вы получаете 200 руб.
Одна машина может доставить 4 плиты в день, а вторая - 8 плит.
Сформулируйте задачу максимизации дохода, если Ваш контракт с водителями предусматривает
* Штраф 400 рублей за разность числа плит, перевезённых машинами:
Штраф = 400 * (P2 – P1).
* Штраф 400 рублей за модуль разности числа плит между водителями.
Штраф = 400 * | P2 – P1 |.
Убедитесь, что Ваша реализация штрафа работает в обе стороны.
Задача 5: разбор идеи. Найдите максимум (x – y) в области, ограниченной
0 < x < 1,
0 < y < 1,
x^2 < y.
Обсуждение.
Решить точно с помощью линейного программирования невозможно:
x^2 < y
не является линейным условием.
Решим задачу приближённо:
Проведём множество касательных к графику
y = x^2
и потребуем, чтобы решение было выше каждой из касательных.
Уравнение касательной к параболе в точке (X1, Y1 = X1^2) :
(y – Y1) = 2 * (x – X1)
-- это действительно прямая,
она проходит через точку (X1, Y1),
и она имеет нужный наклон.
Подробнее – на спецкурсе.
Выберем несколько точек и в каждой проведём касательную:
X1 = 0.1, X2 = 0.2, X3 = 0.3, … X9 = 0.9, X10 = 1.0,
Потребуем, чтобы решение (x, у) было выше каждой из этих касательных
y – Y1 > 2 * (x – X1)
y – Y2 > 2 * (x – X2)
…
Задача 6. Найдите максимум (x – y) в единичном круге: x^2 + y^2 = 1.
Моделирование в задаче про фермера
1) Как зависит оптимально решение в задаче про фермера
* от ёмкости склада?
* от площади поля?
* от допустимых затрат на производство?
Решите задачу при разных ёмкостях склада.
Объясните результаты.
Напоминание
/* Objective function */
max: 143 x +60 y;
/* Constraints */
Cost: +120 x +210 y <= 15000;
Area: +x +y <= 75;
Storage: +110 x +30 y <= 4000;
2) Пусть есть возможность взять кредит.
На что его лучше потратить:
* текущие расходы производства ?
* расширение поля ?
* расширение склада ?
3) Как изменится решение и ответ, если появятся дополнительные ограничения:
* доступность семян: x < … и у < … ;
в каком случае это ограничение существенно?
* личные предпочтения: x > 1.5 y ?
* обязательства по поставкам : x > … и y > …
4) Как изменится решение, если появится возможность использовать новую культуру?
Судоку 4x4 как задача целочисленного линейного программирования.
Необходимо заполнить свободные клетки цифрами от 1 до 4 так, чтобы в каждой строке, в каждом столбце и в каждом малом квадрате 2x2 каждая цифра встречалась бы только один раз.
Сформулируйте на языке LP.
Могут быть полезны бинарные (двоичные) переменные решения;
они могут иметь значения 0 или 1, "да" или "нет".
Пример:
min: -x1 -2 x2 +0.1 x3 +3 x4;
r_1: +x1 +x2 <= 5;
r_2: +2 x1 -x2 >= 0;
r_3: -x1 +3 x2 >= 0;
r_4: +x3 +x4 >= 0.5;
bin x3, x4;
Примеры задач Судоку:
* Найдите хоть одно решение
* Предложите способ найти как можно больше решений каждой из этих задач
* 2 | * *
3 * | * *
- - - - -
* * | 4 3
* 3 | * *
* 2 | * 4
3 * | * *
- - - - -
* * | 4 *
* * | * *
Баскетбольная задача: состав команды
В задаче покрытия множества рассматриваются бинарные (двоичные) переменные решения; то есть они могут иметь значения 0 или 1, "да" или "нет".
Пример:
min: -x1 -2 x2 +0.1 x3 +3 x4;
r_1: +x1 +x2 <= 5;
r_2: +2 x1 -x2 >= 0;
r_3: -x1 +3 x2 >= 0;
r_4: +x3 +x4 >= 0.5;
bin x3, x4;
Условие
Баскетбольный тренер хочет расставить игроков своей команды на игру.
Команда состоит из семи игроков, из которых в игре участие будут принимать пять. Известны способности каждого игрока: передачи, игра в защите, точность бросков и подбор мяча у щита. Шкала от 1 (плохо) до 3 (отлично)
Игроки могут выступать в роли защитника (B - back-field), центрового (M - mid-field) и нападающего (F - front-field). Роли каждого игрока и их способности показаны в Таблице.
Таблица. Игроки и их способности
Игрок | Амплуа | Передачи | Броски | Подбор | Защита |
1 | B | 3 | 3 | 1 | 3 |
2 | M | 2 | 1 | 3 | 2 |
3 | BM | 2 | 3 | 2 | 2 |
4 | MF | 1 | 3 | 3 | 1 |
5 | BF | 1 | 3 | 1 | 2 |
6 | MF | 3 | 1 | 2 | 3 |
7 | BF | 3 | 2 | 2 | 1 |
Все пять выбранных игроков должны удовлетворять следующим ограничивающим условиям:
Цель - максимально усилить игру в защите.
Удовлетворите мои потребности в питании с наименьшими затратами.
Моя диета требует, чтобы вся пища, которую я ем, принадлежала к одной из четырех "основных пищевых групп": шоколадный кекс, мороженое, газированная вода и творожный пудинг. В магазине есть: шоколадное пирожное с орехами, шоколадное мороженое, кола и ананасовый творожный пудинг.
Одно пирожное стоит $0.50,
одна порция мороженого стоит $0.20,
одна бутылка колы стоит $0.30,
и один кусок пудинга стоит $0.80.
Каждый день я должен получать не менее 500 калорий, 6 унций (1 унция = 28,35 грамм) шоколада, 10 унций сахара и 8 унций жира.
Содержание питательных веществ на единицу для каждого вида пищи приведено в таблице ниже.
Для обобщения важной информации по задаче:
Стоимость пищи за единицу
Ежедневные потребности в пище
Содержание питательных веществ на единицу для каждого вида пищи