21-й Турнир им. Ломоносова

Турнир им. М.В. Ломоносова - ежегодное многопредметное соревнование по математике, физике, наукам о Земле, химии, биологии, истории, лингвистике. Цель Турнира - дать участникам материал для размышлений и подтолкнуть интересующихся к серьезным занятиям. Турнир проводится Международным оргкомитетом Турнира городов при поддержке МИПКРО (Московского Института повышения квалификации работников образования), Московским Центром непрерывного математического образования, вузами и школами Москвы.

На данной странице вы можете ознакомиться со следующей информацией:
(дата последнего обновления 10.11.1998)

• Задания конкурса по биологии
• Конкурс по астрономии и наукам о Земле (задания, ответы, комментарии, типичные ошибки, перлы школьников)
• Задачи конкурса по химии и их краткие решения.
• Конкурс по истории: задачи, текст с историческими ошибками, решения задач, список ошибок с комментариями.
• Конкурс по математическим играм: условия, решения, инструкция для проводящих конкурс
• Конкурс по математике: задачи и их решения
• Задачи и задания конкурса по физике
• Конкурс по лингвистике: задачи и их решения
• СПИСОК ПОБЕДИТЕЛЕЙ ТУРНИРА (Москва)
• Информация о закрытии Турнира и награждени успешно выступивших участников (15.11.1998)
• Информация об осеннем туре 20 Международного математического Турнира Городов (состоялся 25.10.1998; ссылка)
• Информация о других мероприятиях для школьников, проводимых организаторами Турнира
  • Разбор задач конкурса по физике
  • Лингвистическая олимпиада
  • Факультатив(кружок) по линвистике при РГГУ
  • Математический кружок МЦНМО
  • Математический кружок 57 школы
  • Малый мехмат
  • Вечерние школы для семиклассников Московской гимназии на Юго-Западе N1543 (бывш. 43 школа)
    • Вечерняя математическая школа
    • Вечерняя историко-литературная школа
    • Вечерняя биологическая школа
• Контактные данные оргкомитета Турнира

Можно скачать ZIP-архив (118 КБ) со всеми файлами, входящими в состав данной страницы, и потом ознакомиться с ней в режиме off-line.

21-й Турнир им. М.В. Ломоносова состоялся в воскресенье, 27 сентября 1998 года. В нём приняли участие более 2000 школьников (зарегистрировались 1926), из них 821 стали победителями в различных конкурсах.

Турнир проводился в Московском авиационном институте, Российском государственном гуманитарном университете, Московском Центре непрерывного математического образования, московских гимназиях NN 1543, 1567, московском Лицее информационных технологий, московских школах NN 26, 444, 491, 520, 602(Зеленоград), 905, 1180, 1678.

Турнир им. М.В. Ломоносова состоит из нескольких конкурсов. Во всех участвовать не обязательно.
Все конкурсы по различным предметам проводятся одновременно в разных аудиториях. Школьники могут в любое время переходить из аудитории в аудиторию и принять участие в любом количестве конкурсов, победители определяются отдельно в каждом конкурсе.
Один конкурс (математические игры) - устный, остальные - письменные.

Предполагаемый возраст участников - 7 класс и старше, включая 11.
В Турнире могут принимать участие и более младшие школьники (в прошлые годы некоторые из них также становились победителями).
Следует, однако, учесть, что специальных заданий для учащихся 6 классов и младше не будет; учащимся этих классов имет смысл приходить на Турнир, если они морально готовы выполнять задания 7 класса.

Участие в Турнире для школьников является добровольным и бесплатным.
Если где-то это окажется не так - просьба сообщать в оргкомитет.

Задания конкурса по биологии

1. Как отличается поведение кошек и собак? С чем это связано?
2. На биологической экскурсии вы обнаружили неизвестный ранее организм; при внимательном изучении оказалось, что рта у организма нет. Как могло бы питаться это существо? По каким внешним признакам можно об этом судить?
3. Какие из перечисленных признаков пригодились бы растениям из засушливых мест? Почему вы так думаете? Назовите известные растения с такими признаками.

   - отсутствие листьев		- толстые мясистые листья
   - луковица		- опушение на листьях и стеблях
   - толстый эпидермис		- тонкие крупные листья
   - эфирные масла в побегах		- листья с оттянутыми кончиками
   - восковой налёт		- тонкие вьющиеся стебли
   - колючки вместо листьев		- яркие сочные плоды
   - толстый зелёный стебель		- стебель с воздушными полостями
   - неяркий венчик		- многочисленные листья
   - сухие летающие плоды		- душистые цветки, открывающиеся ночью

   
   
4. Где в клетке "работает" мембрана? Какие особенности её строения при этом используются? Все ли мембраны в клетке одинаковы?
5. Задание не приводится, так как по ошибке не было напечатано в листках с заданиями, которые раздавались школьникам во время Турнира.
6. Какое значение в жизни растений может играть яркая окраска плодов, цветов, листьев? Назовите, если возможно, вещества, которые обусловливают яркую окраску разных частей растения?
7. Как вы знаете, информация о структуре белков закодирована в структуре ДНК. Она переписывается на молекулу информационной РНК, которая транспортируется в цитоплазму, и там на её основе синтезируется белок. Оказалось, однако, что многие белки затем транспортируются обратно, в ядро. Как вы думаете, что они там могут делать? Почему они не синтезируются в ядре?
8. В Центральной Африке в ряде близко расположенных деревень у жителей обнаружена неизвестная ранее болезнь. Вы приехали в этот район в составе экспедиции Всемирной Организации Здравоохранения в качестве эпидемиолога. Ваша цель - выяснить причину заболевания. Каков план ваших действий?
9. Известно, что срубленное дерево не гниёт в двух случаях: если сохраняется в совершенно сухом месте или если оно полностью утоплено в воде. Как это объяснить?
10. Как могли бы питаться птицы с такими клювами?
    
11. На Земле есть места, где никогда не растёт лес, это - тундра, степи. Есть такие места и в средней полосе России - под городом Владимиром, так называемое Владимиро-Суздальское ополье. Каковы могут быть причины (или причина) такого безлесья?

Задания конкурса по астрономии и наукам о Земле

1. Пролетая мимо Плутона, космонавт решил немного прогуляться в открытом космосе и заодно почитать вечернюю газету. Сможет ли он это сделать?
2. Есть ли на других планетах моря и океаны? А вулканы?
3. Во время сборки орбитальной станции "Мир" один монтажник бросил другому гаечный ключ, но промахнулся. Какова дальнейшая динамическая судьба ключа, станции и монтажника?
4. Почему так трудно предсказывать землетрясения?
5. 20 июня 1998 года над Москвой пронёсся сильный ураган. Почему сломанные деревья были повалены не везде, а в некоторых местах в виде полос? Почему образовался подобный ураган, каковы были его ширина у поверхности и скорость ветра? Чем он отличался от тропических тайфунов?
6. 23 сентября астрономы отмечают день осеннего равноденствия. Почему весеннее равноденствие (21 марта) происходит на 2 дня раньше?
7. Нетрудно подсчитать, что на поверхности Земли сила притяжения к Солнцу намного больше, чем к Луне. Почему же лунные приливы выше солнечных?
8. Наиболее красивые и удобные для обзора места в Москве (Крылатское, Поклонная гора, Воробьёвы горы, Коломенское) расположены на правом берегу Москвы-реки. Случайно ли это?
9. Известно, что можно определить стороны света по часовой стрелке. Каким образом это можно сделать, находясь в Эфиопии? А в Новой Зеландии?
10. Смогут ли жители лунных поселений наблюдать корону Солнца во время затмений?

Ответы на задания конкурса по астрономии и наукам о Земле (с комментариями и указанием типичных ошибок)

1. Вопрос: Пролетая мимо Плутона, космонавт решил немного прогуляться в открытом космосе и заодно почитать вечернюю газету. Сможет ли он это сделать ?

   Ответ: Космонавт у Плутона может читать газету и без искусственного освещения.

   Критерии оценки: Да-1 балл; Указано, что освещенность достаточная -1; Указаны дополнительные необходимые условия-1; Итого- 3 балла.

   Комментарий: Как известно, расстояние от Солнца до Плутона в 40 раз больше, чем до Земли. Соответственно, освещенность, которая уменьшается от расстояния как R^-2, в открытом космосе около Плутона в 1600 раз меньше, чем около Земли. Оценим, достаточно ли этого для чтения ? При этом будем считать, что минимальный уровень освещенности для чтения соответствует освещенности от полной Луны.

   Способ 1. Видимая звездная величина (логарифмическая шкала яркостей небесных объектов) полной Луны равна - 13 ^m. Видимая звездная величина Солнца на Земле (без поглощения в атмосфере) составляет - 27 ^m, что на 14 звездных величин ярче. Разница яркостей на 1 звездную величину составляет 2.512 раз, на 4 - в 40 раз, на 5 величин - в 100 раз. Соответственно, для земного наблюдателя Солнце ярче Луны на 14=5+5+4 величин, или в 100х100х40=400000 раз, а около Плутона создает примерно в 400000/1600 = 250 раз большую освещенность, чем полная Луна на Земле. Это соответствует ранним гражданским сумеркам или белым ночам на Земле и вполне достаточно для чтения.

   Способ 2. Соотношение освещенностей от Солнца и полной Луны на Земле можно приблизительно оценить и без знания их видимых звездных величин, поскольку известно, что Луна светит отраженным солнечным светом, а угловые размеры Луны и Солнца совпадают. Для этого Солнце от его действительного рахмера (радиус 700 тыс км) увеличим до 150 млн км, т.е. до радиуса орбиты Земли(но только мысленно !). Поверхностная яркость "раздутого Солнца" уменьшится как квадрат увеличения его радиуса, т.е. в 46200 раз, Соответственно и Луна, как отражатель света на этом расстоянии от истинного Солнца, во столько же раз получает его меньше. Кроме этого, сама Луна отнюдь не зеркало, а весьма неровное каменистое тело, и отражает всего 7 % от падающего на нее света, т.е. в итоге светит слабее Солнца на Земле в 660000 раз, или в 400 раз слабее, чем Солнце на Плутоне.

   Кроме этого, желательно указать в ответе, что для прогулки в открытом космосе около Плутона необходим скафандр со всеми системами жизнеобеспечения космонавта, что газету (бумажную) в свободном полете разворачивать и читать можно, поскольку нет воздуха и ветра, и что такая газета должна передаваться электронными средствами связи и печататься непосредственно на борту корабля, иначе она через короткое время из "вечерней" станет "вчерашней", а затем и вовсе "исторической". Кстати, время пересылки радиосигнала от Земли до Плутона составляет примерно 5 часов 20 минут.

   Типичные ошибки:
   - На Плутон еще не летают;
   - На Плутоне "слишком темно" или "совсем темно";
   - В открытом космосе космонавт "замерзнет", или " в невесомости нельзя гулять", или нельзя "достать газету из кармана";
   - В космосе не бывает вечера; на разных планетах вечер наступает в разное время;

   Нетривиальные версии:
   - Плутон еще не открыт;
   - Космонавт сможет это делать только в далеком будущем. т.к. до Плутона несколько световых лет;
   - Откуда в космосе вечерняя газета? Космонавт нигде не сможет купить газету;
   - Газеты в космосе не летают ! ;
   - Читать старую газету неинтересно;
   - В космосе нет воздуха, и солнечный свет не рассеивается;
   - Свет от Солнца до Плутона не доходит, т.к. рассеивается на космической пыли;
   - В космосе мельчайшие частицы изорвут всю газету в клочья;
   - Газета в космосе может загореться;
   - Газета в космосе испортится от рациации;
   - В безвоздушном пространстве газета и ее краска разлетится на молекулы;
   - В безвоздушном пространстве газета станет круглой формы;
   - В космосе очень сжатый воздух, и его газета сожмется;
   - Газета и без кислорода хорошо читается;
   - Т.к. у корабля, космонавта и газеты очень разные массы, то после встречи с Плутоном их скорости тоже будут сильно разные, и они разлетятся в разные стороны;
   - Разные силы притяжения разорвут газету;
   - На Плутоне нет притяжения, и космонавт улетит в космос;
   - На Плутоне очень сильное притяжение, и космонавта с газетой раздавит;
   - Космонавт не может прогуляться, а только пролетаться;
   - Из-за невесомости космонавт сможет передвигаться маленькими прыжками;
   - В космосе принять вертикальное положение и сделать вид, что прогуливаешся, очень трудно;
   - Космонавт закружится, испугается и отпустит газету;
   - Космонавт не сможет спокойно почитать газету, т.к. его будет мотать из стороны в сторону;
   - Космонавт успеет прочитать газету, т.к. на Плутоне вечер длится намного дольше, чем на Земле;
   - Космонавт читать газету сможет, т.к. он умеет читать;
   - Космонавт должен работать, а не газеты читать.
   
   

2. Вопрос:Есть ли на других планетах моря и океаны ? А вулканы ?

   Ответ: Вулканы, моря и океаны есть и на планетах Солнечной системы, и могут существовать в иных планетных системах.

   Критерии оценки: Да-1 балл; Приведены конкретные примеры (Луна, Марс, Венера, Ио, Ганимед) - 1; Указаны необходимые общефизические условия для иных планет -1; Итого- 3 балла.

   Комментарий: Морем (океаном) следует называть объект в поверхностных слоях планетного тела, состоящий из жидкой (квазижидкой) среды и занимающий существенную часть планеты. В известном смысле можно сказать, что практически на всех планетах, т.е. на астрономических телах с массой более 10 ²⁵ г, моря и океаны существуют или могут существовать, но, разумеется не только из воды (H₂O), а также из иных жидких (или полужидких) веществ. Даже по отношению к нормальным звездам поэческий образ М.В.Ломоносова, сравнившего Солнце с огненным океаном, имеет право на существование, т.к. движение высокотемпературной плазмы в сильных магнитных полях, что типично для поверхностных слоев звезд, имеет сильную турбуленцию и во многом похоже на поведение жидких сред. На всех планетах земной группы имеются моря, образованные разливами жидкой магмы, из которых наиболее известны моря на Луне. На поверхности Марса имеются следы мощных жидких потоков, следовательно, ранее могли существовать и моря (из воды?). Широко известные вулканы на Ио, как предполагают, питаются приповерхностными "морями" из жидкой серы и ее соединений. Значительный жидкий слой (из воды?) предполагается под ледяной коркой на Ганимеде. Все планеты-гиганты и их массивные спутники должны иметь жидкие слои, составляющие в некоторых случаях основную часть этих планет и состоящие из метана (CH₄), аммиака (NH₃), водорода (H₂) и иных летучих соединений. Следует также указать, что необходимым условием существования на планете поверхностных немагматических морей является наличие достаточно мощной атмосферы.

   Вулканом следует называть явление выброса жидких, полужидких или газообразных веществ на поверхность планетного тела сквозь разломы его твердых оболочек, создающее новые формы рельефа. Наиболее известные магматические вулканы находятся на Луне (недействующие), самый высокий вулкан солнечной системы - гора Олимп (25 км высоты),- на Марсе, а также на Венере. Активно действующие вулканы наблюдались на Ио (из сернистых соединений); на Луне отмечались выбросы газов в центре кратеров. Большое Красное пятно Юпитера, по-видимому, может быть связано с выбросом потока вещества из глубинных слоев планеты. В качестве минимально предельного случая "вулкана" можно рассматривать газовые струи, бьющие сквозь поверхностую корку на ядрах комет, как это наблюдалось для ядер комет Галлея в 1986 г. и Хейла-Боппа в 1997 г.

   Типичные ошибки:
   - морей нет;

   Нетривиальные версии:
   - На других планетах все, как у нас: и моря есть, но без воды; и вулканы есть, но не работают;
   - На других планетах не то что морей и океанов, а даже и растительности-то нет;
   - Притяжение есть только у Земли, а у других планет - нет, поэтому и воды там нет;
   - Морей нет, зато на Венере обнаружили лед;
   - Нет, потому что они там вовсе не нужны;
   - Вулкан существует на планете Маленького принца Экзепюри;
   
   

3. Вопрос:Во время сборки орбитальной станции "Мир" один монтажник бросил другому гаечный ключ, но промахнулся. Какова дальнейшая динамическая судьба ключа, станции и монтажника ?

   Ответ: Ключ выходит на новую самостоятельную орбиту вокруг Земли, параметры которой определяются направлением броска, монтажник летит в противоположную сторону с пропорционально меньшей скоростью, станция продолжает свой полет.

   Критерии оценки: Указан факт разлета в невесомости в разные стороны -1 балл; Указаны различные скорости по закону сохранения импульса -1; Указан факт выхода ключа на новую орбиту в зависимости от направления броска -1; Указан факт возврата через один орбитальный оборот - 1; Рассмотрен случай внутри станции -1; Итого- 5 баллов.

   Комментарий: В качестве побочных случаев для данной задачи укажем на ситуацию в сборочном цехе на земле ( в этом случае ключ упадет на пол, а кто-то из монтажников его подберет) и внутри станции на орбите (ключ будет плавать в невесомости внутри станции и обо всех стукаться).

   Основная ситуация, конечно, предполагает, что это происходит в открытом космосе вне станции, которая, будем считать, движется по круговой орбите вокруг Земли. В соответствии с законом сохранения импульса для системы "ключ-монтажник", оба объекта после броска начнут двигаться в противоположные стороны со скоростями, обратно пропорциональными их массам. При массе ключа 1 кг и скорости броска 5 м/с скорость монтажника относительно станции составит до 5 см/с, что заведомо не превосходит скорости его обычных движений. Станция, очевидно, также продолжит свой плановый полет. Ключ же выйдет на самостоятельную эллиптическую орбиту вокруг Земли, параметры которой будут зависеть от направления броска.

   При броске "вперед" (по направлению полета станции) ключ приобретает дополнительную кинетическую энергию и выйдет на более высокую относительно станции (и монтажника) орбиту с несколько большим периодом обращения вокруг Земли, перигей которой будет находится в точке броска, а апогей - через полоборота. При броске "назад", орбита ключа будет в целом ниже орбиты станции, период несколько уменьшится, а апогей новой орбиты будет в точке броска. При бросках "вверх" и "вниз" большие полуоси новых орбит ключа будут равны радиусу орбиты станции, а его период равен орбитальному периоду станции, так что ключ будет полоборота лететь "выше" станции, а полоборота - ниже ее, сближаясь с ней через каждый орбитальный оборот. При бросках "вбок" ("вправо" или "влево" относительно направления полета станции и параллельно поверхности Земли) новая орбита ключа сохраняет прежний радиус и период, но несколько изменяет положение плоскости орбиты, так что ключ "отлетает" от станции "вбок" и возвращается вновь к ней через каждые полоборота.

   При высоте полета станции 300 км над поверхностью Земли, ее скорость будет равна 7.77 км/с, а ее орбитальный период составит около 90 мин. "Мини-орбита" ключа вокруг станции при таком же периоде составит около 8.6 км в диаметре, и при любых бросках "поперек" движения станции ключ, описав такую мини-орбиту, возвращается через 45 минут к станции, как бумеранг (монтажники, внимание! ). Кроме этого, при бросках "вперед" или "назад" орбитальный период ключа относительно периода станции за счет перехода на более высокую или более низкую орбиту изменится на 0.00037 , что соответствует дополнительной скорости ключа "вдоль" орбиты станции в 2.9 м/с. За счет этого изменения орбитальной скорости, ключ при броске "вперед" за каждый орбитальный оборот будет отставать от станции на 15.5 км, а при броске "назад" - обгонять ее на такую же величину.

   Таким образом, траектория ключа относительно станции при броске, например, "вперед" будет представлять собой вытянутую циклоиду: сначала ключ полетит вперед по направлению броска со скоростью 5 м/с, затем начнет тормозить и отклоняться "вверх", через полоборота наберет максимальную высоту над станцией около 5 км и максимальную скорость "назад", затем вновь начнет "снижаться" и "ускоряться", однако "опустится" на первоначальную орбиту станции, сильно от нее отстав (на 15 км), и больше ее уже не догонит, т.к. пойдет на следующий виток циклоиды. Существует некоторая положительная вероятность последующей встречи ключа и станции (следующее после броска сближение на орбите ожидается через 167.5 суток), однако с учетом размеров станции (около 50 м) и существенной неустойчивости реальных орбит, эта вероятность пренебрежимо мала. При броске "назад" ключ летит "назад", "вниз", "сильно вперед", "вверх", и в итоге за один орбитальный период на 15 км станцию "обгоняет".

   Но в любом из рассмотренных случаев монтажник, бросивший ключ, получит строгое должностное взыскание за нарушение техники безопасности монтажных работ, засорение космического пространства посторонними предметами, и, скорее всего, будет списан на Землю.

   Типичные ошибки:
   - ключ упадет на Землю;
   - ключ в невесомости повиснет на одном месте;
   - ключ полетит прямо;
   - монтажник полетит вслед за ключом:
   - станция упадет в Тихий океан;
   - станция может развалиться, если ее не завинтить;

   Нетривиальные версии:
   - Мы-то знаем, что "Мир" достроили;
   - Ключу ничего не будет, и станции тоже;
   - Если ключ ударится о "Мир", то "Мир" может подвинуться;
   - Ключ упадет в ненужном месте;
   - Ключ может провалиться и куда-нибудь затеряться;
   - Гаечный ключ придется ловить сачком;
   - Т.к. в космосе нет ни трения, ни земного притяжения, ключ улетит в бесконечность;
   - Из-за невесомости в космосе никогда нельзя попасть туда, куда нужно;
   - Монтажник останется жив, и ключ тоже;
   - Монтажники достроили станцию и улетели домой;
   - Монтажнику придется купить новый ключ;
   - Если монтажник потянется за ключом. он может не удержаться;
   - Монтажник преодолел инерцию и полетел, увлекая за собой станцию;
   - Монтажник будет разочарован;
   - Монтажника будут долго ругать;
   - Другой монтажник. от которого отскочил ключ, остался жив, живет сейчас и часто вспоминает этот случай;
   - Монтажник начнет гоняться за ключом в безвоздушном пространстве и когда-нибудь его поймает;
   - Если монтажник сообщит ключу вторую космическую скорость. то ключ начнет вращаться вокруг Солнца, а монтажник упадет на Землю;
   
   

4. Вопрос: Почему так трудно предсказывать землетрясения ?

   Ответ: Землетрясения имеют неявные (скрытые) причины, случайный характер и очень быстрое развитие во времени.

   Критерии оценки: Указан смысл предсказания (место, время, магнитуда) -1 балл; Указан случайный характер процесса -1; Указаны геодинамические причины землетрясений -1; Указан факт недоступности области процесса и иные технические проблемы - 1; Итого- 4 балла.

   Комментарий: Первопричиной всех тектонических явлений на поверхности Земли (и других планет), в т.ч. землетрясений, является взаимное движение литосферных плит земной коры с типичными скоростями 1-2 см/год (максимальное значение до 10 см/год). Это равномерное в своей основе движение кусков коры приводит к постоянному накоплению механических напряжений в горных породах в зонах геологических разломов, которые время от времени, случайным образом сбрасываются за счет разрушения (растрескивания) пород в очаге землетрясения и быстрого "проскакивания" соседних слоев друг относительно друга на расстояния до нескольких метров. Вследствие: а) недоступности очага землетрясения для непосредственного наблюдения и измерений ( очаги землетрясений располагаются на глубинах до 33 км), б) непредсказуемости структурного состояния пород и их предела прочности в данном конкретном месте и в данных условиях, а также в) кратковременности самого процесса разрушения и тектонической подвижки (скорости сейсмических волн достигают 8 км/с, т.е. могут превышать 1-ю космическую скорость, а средняя продолжительность землетрясения на поверхности 5-10 с),- можно сказать, что предсказание землетрясения, т.е. указание для будущего события его места (эпицентра), времени и силы (магнитуды), является теоретически невозможным. Единственное, что возможно для параметров предстоящего землетрясения, это их вероятностные оценки. Для этого применяются методы сейсмического районирования и наблюдения предвестников землетрясений.

   Сейсмическое районирование означает определение границ сейсмически опасных районов на поверхности Земли с указанием максимальной магнитуды (М) землетрясения, возможного в данном районе. Оно осуществляется на основе глобальной геодинамики и сведений о всех известных предыдущих землетрясениях, и применяется в первую очередь для создания норм сейсмостойкого строительства и сейсмобезопасности. В среднем на Земле каждый год происходит землетрясение силой более 8.0 М по Рихтеру, приводящее к разрушению большинства зданий в его эпицентре. Известно также, что при катастрофических землетрясениях ( Х11 балов по Меркалли или 8.6 М Рихтера), которые могут повторяться до 10 раз в столетие, наблюдаются колебания грунта с ускорением до 10 ⁵ см/с, что почти в 100 раз больше ускорения свободного падения, подбрасывание предметов в воздух и т.н. "земляные волны" на поверхности.

   Во всех сейсмически опасных районах ведется мониторинг предвестников землетрясений, среди которых можно назвать: рои слабых предшествующих толчков; микродвижения (до 1 мм/год) и наклоны земной поверхности (до 10 ^-8 рад); деформации горных пород; изменения уровней грунтовых вод и содержания в них радона (радиоактивный газ); изменения скоростей распространения сейсмических волн; локальные изменения магнитного поля и электрического сопротивления горных пород; и даже специфические возмущения в ионосфере. В качестве неинструментального индикатора воздействия предвестников землетрясений на живые организмы известно аномальное поведение животных. Однако, очевидно, что все предвестники сигнализируют тем или иным образом лишь о факте нарастания механических напряжений в земной коре, но не дают информации о "спусковом механизме" предстоящего землетрясения, его моменте во времени и количестве одновременно высвобождаемой энергии. Таким образом, в современных условиях можно утверждать, что большинство будущих землетрясений предсказано, к сожалению, не будет. Кроме этого, в силу особой социальной значимости землетрясения, его ошибочный (несостоявшийся) прогноз является неприемлемым.

   Сильнейшие инструментально измеренные землетрясения с магнитудой 8.9 происходили 31.01.1906г. около Эквадора (продолжительностью около 3 минут) и 03.03.1933г. около Санрику, Япония. Каждое из них выделяло энергию в 10²⁵ эрг, что превосходит энергию водородной бомбы. В среднем 10000 человек ежегодно погибает вследствие землетрясений. Наиболее катастрофическое землетрясение в ХХ веке произошло 28.07.1976г. в г.Тяншань, Китай ( 7.8 М, 243000 погибших), а в истории человечества - 23.01.1556г. в Шаньси, Китай ( 8.0 М, 830000 погибших). Общее энерговыделение землетрясений на Земле - 10 ²⁶ эрг/год.

   Типичные ошибки:
   - Природу вообще трудно предсказывать;

   Нетривиальные версии:
   - Землетрясения происходят в тропосфере и ни от чего не зависят;
   - Землетрясение состоит из нескольких толчков: один предупредительный, а остальные - разрушающие;
   - Т.к. литосферных плит целых 7, то какая из них подвинется следующая. никто не знает;
   - Землетрясение - это химический процесс; солнечные лучи воздействют на почву, и она разламывается;
   
   

5. Вопрос:20 июня 1998 года над Москвой пронесся мощный ураган. Почему сломанные деревья были повалены не везде, а в некоторых местах в виде "полос" ? Почему образовался подобный ураган, какова была его ширина у поверхности земли и скорость ветра ? Чем он отличается от тропических тайфунов ?

   Ответ: Ураганный ветер (до 30 м/с) возник из-за столкновения двух атмосферных фронтов с большой разностью температур и давления воздуха, имел зону действия около 30 х 300 км и причинил разрушения в местах прохождения наиболее быстрых вихрей воздуха.

   Критерии оценки: Указан вихревой характер самого воздушного потока-1 балл; Указано столкновение атмосферных фронтов -1; Указаны основные параметры шквала -1; Указано, что тайфуны имеют природу большого самоподдерживающегося вихря и регулярны -1; Итого- 4 балла.

   Комментарий: Любой поток воздуха, а тем более такой мощный как ураган, имеет не равномерный характер, а вихревой. Примеры таких вихрей можно наблюдать на клубах дыма, облаках и других видимых потоках. Их размеры в свободной атмосфере составляют от сотен до десятков метров. Поток в целом характеризуется некоторой средней скоростью, а скорость движения воздуха в данной точке - ее моментальной скоростью. Моментальная скорость варьируется относительно средней в достаточно широких пределах и может значительно ее превышать (иногда в несколько раз). Вместе с тем известно, что сила аэродинамического сопротивления любого тела в потоке пропорциональна квадрату скорости потока. Таким образом, если моментальная скорость воздуха в локальном вихре превысит среднюю, например, в 3 раза, то сила давления на препятствия этому потоку может возрасти почти в 10 раз. Поэтому понятно, что вывал деревьев происходит не повсеместно, а в тех зонах, где более "быстрая" половина вихрей касалась и "прокатывалась" по поверхности земли, шириной в десятки и длиной в сотни метров. Подобное же воздействие при шквалистом ветре можно наглядно видеть на поверхности небольших водоемов или на равномерно засеянном поле.

   Ураганные ветры на средних равнинах могут возникать из-за столкновения двух атмосферных фронтов с сильно различными температурами и давлениями воздуха в них. Горизонтальные размеры таких фронтов составляют сотни километров. 20.06.98 г. над Москвой встретились воздушные массы относительно сухого воздуха с температурой + 35 ⁰С и влажного с температурой + 10-15 ⁰С. Когда вследствие взаимного движения фронтов более тяжелый холодный воздух оказался над более легким теплым, возникли условия динамической неустойчивости; теплый воздух начал подниматься вверх, а холодный - падать вниз с большой скоростью, образуя мощные потоки и вихри. Ширина полосы разрушительного урагана составила 20-30 км, протяженность - до 300 км, скорость ветра - до 30 м/с. Повторяемость подобных ураганов, иногда сопровождаемых также смерчами, для конкретной местности составляет несколько раз в столетие. В условиях городской застройки воздушные потоки в приземном слое могут как ускоряться в узкостях, так и тормозится зданиями, но этот фактор не является главным; нередко в одинаковых соседних дворах картина была совершенно различной: от отсутствия повреждений до полного вывала деревьев.

   Тропические тайфуны, напротив, являются типичным явлением и повторяются десятки раз за сезон. Они образуются в тропических зонах, где Солнце светит отвесно и сильно нагревает поверхность и нижний слой воздуха. При этом неравновесные условия в атмосфере создаются практически повсеместно, особенно над ровной поверхностью океана. Любая спонтанно возникшая конвективная ячейка перетекания нагретого воздуха вверх, а холодного - вниз, в этих условиях может разрастаться, увеличивая свой масштаб и мощность. Двигаясь по океану, тайфун приобретает устойчивую спиральную структуру, вовлекающую в себя все новые и новые неустойчивые области воздуха, и высвобождаемую потенциальную энергию переводит в скорость ветра, которая может достигать 60 м/с (более 200 км/час). Тайфуны вызывают в океане волнение до 20 м высотой, наводнения за счет большого количества осадков и нагонов воды, многочисленные и катастрофические разрушения.

   Типичные ошибки:
   - Деревья падали на открытых местах, а дома ветер задерживали;
   - В городе здания создают "аэродинамические коридоры", где ветер усиливается;
   - Падают старые деревья;
   - Деревья падают рядами, т.к. одно падает на другое;
   - Деревья падают рядами, т.к. они в городе рядами посажены.

   Нетривиальные версии:
   - Где урагану удобнее ломать деревья, там он и действует;
   - Ураган, как единое тело, идет в одном направлении;
   - Деревья падали там, где сила притяжения Земли немного больше;
   - Скорость ветра указать не могу, т.к. была в это время на даче;
   - Ураган обычно подхватывает деревья и долго несет их в себе, а потом, ослабевая, опускал их все сразу на землю;
   - Когда дерево падает на землю, оно создает такой грохот, что другие деревья не выдерживают и тоже начинают падать;
   - Ураган образовался из-за сильного скопления туч на небе, для разгона которых потребовался сильный ветер;
   - Молекулы воздуха шли с большой скоростью в виде групп, т.к. Москва - не лысое поле;
   
   

6. Вопрос:23 сентября астрономы отмечают День осеннего равноденствия. Почему весеннее равноденствие (21 марта) происходит на 2 дня раньше ?

   Ответ: Из-за эллиптической формы своей орбиты Земля одну ее половину проходит быстрее, чем другую.

   Критерии оценки: Указан факт эксцентриситета орбиты Земли -1; Дано описание движения Земли по орбите и смена сезонов -1; Итого- 2 балла.

   Комментарий: На самом деле, если просто подсчитать число дней по календарю, то за счет месяца февраля, укороченного на 3 дня, и за счет "дополнительного" 31-го дня в августе (в честь Августа), весеннее равноденствие наступает не на 2 дня, а на 7 или 8 дней раньше в зависимости от високосного года. Так что неравномерность нашего календаря не только не является причиной этого, а наоборот, будучи отражением неравномерного движения Солнца, остается все же "недостаточной" для компенсации этого разрыва. В 1998 году Солнце пересекло небесный экватор снизу вверх (т.е. изменило свое склонение с отрицательного на положительное) 20 марта в 19 часов 54 минуты 31 секунду всемирного времени (UT), а в обратном направлении - 23 сентября в 5^h37^m11^s UT. Таким образом, период от весеннего равноденствия до осеннего, когда Солнце находилось выше небесного экватора, составил 186.4046 суток. При общей продолжительности года в григорианском календаре в 365.2425 суток, на противоположный период от осеннего до весеннего равноденствия остается 178.8378 суток, или на 7.5668 дня ( ! ) меньше.

   Происходит это из-за того, что орбита Земли вокруг Солнца не круговая, а эллиптическая с эксцентриситетом (т.е. смещением фокуса относительно центра орбиты) 0.017. Поэтому в точке перигелия (ближайшей к Солнцу), которую Земля проходила в 1998 году 04 января в 21^h15^m01^s UT, ее расстояние от Солнца составляло 147099552 км, а в противоположной точке орбиты, в афелии, где Земля была 03 июля в 23^h50^m11^s UT, это расстояние было 152095605 км, т.е. на 5 млн км больше. Это изменение расстояния до Солнца также хорошо заметно по изменению его видимого углового размера, который от 32'34" в январе уменьшается до 31'30" в июле. Так что можно обоснованно утверждать, что на Земле самый "солнечный и теплый" месяц в году - январь, а самый "холодный" - июль.

   В соответствии со 2-м законом Кеплера, момент количества движения тела по орбите постоянен, а соответственно, его орбитальная скорость обратно пропорциональна радиусу-вектору. Поэтому скорость движения Земли по орбите также не постоянна, а изменяется от 29.5 км/с в верхней части орбиты (июль) до 30.3 км/с в нижней (январь). Соответственно, и расстояние от точки осеннего равноденствия на орбите до весеннего Земля проходит пропорционально быстрее, чем противоположную, летнюю часть.

   Типичные ошибки:
   - Потому, что в феврале на 2 дня меньше;
   - Из-за неравномерного календаря; первые три месяца короче, чем последние;
   - Потому, что солнечный год длиннее календарного;
   - Потому что календарный год отличается от звездного;
   - Потому что звездные сутки короче солнечных;

   Нетривиальные версии:
   - Потому что числа идут: 23, 22, 21, 22;
   - Из-за того, что часто меняли календарь;
   - Для того, чтобы быстрее лето наступало;
   - Т.к. весна - это переход от холодного времени года к теплому, а наша планета все ближе и ближе к Солнцу;
   - Из-за того, что Земля не круглая, а в виде яйца;
   - Первый день Солнце подходит к зениту, ночь оно в зените, а на второй день тихо отходит;
   - В разных частях света равноденствия происходят в разное время;
   - Так как бывают более короткие и боле длинные дни;
   - Т.к. орбита Земли не круглая, то одна половина ее короче, чем другая;
   - Потому что угол падения солнечных лучей быстрее увеличиваеся, чем уменьшается;
   
   

7. Вопрос:Нетрудно подсчитать, что на поверхности Земли сила притяжения к Солнцу намного больше, чем к Луне. Почему же лунные приливы выше солнечных ?

   Ответ: Поскольку Луна существенно ближе к Земле, чем Солнце, то лунная приливная сила оказывается больше.

   Критерии оценки: Указана природа лунных и солнечных приливов -1; Указано, что близость Луны принципиальна -1; Указана зависимость приливных сил, как R^-3 - 2 балла; Итого- 4 балла.

   Комментарий: Сила гравитационного притяжения пропорциональна массе M приягивающего тела и обратно пропорциональная квадрату расстояния R до него. Соответственно, на поверхности Земли сила притяжения к самой Земле ( M_З = 6 10²⁷г, R_З = 6378 км) составляет 1 g , к Солнцу ( M_С= 2 10³³г, R_С= 150 10⁶ км) - 0.00058 g, а к Луне ( M_Л= 7 10²⁵г, R_Л= 384 10³ км) - всего 0.0000031 g, т.е. в 190 раз слабее, чем к Солнцу. Очевидно также, что в однородном силовом поле никаких приливов не будет.

   Однако, поле тяготения не является однородным, а имеет центр в притягивающей массе M. Соответственно, для любого тела с конечными размерами будет существовать разница сил тяготения на противоположных краях, которая и называется приливной силой. Нетрудно показать, что приливная сила, как производная от силы тяготения, обратно пропорциональна третьей степени расстояния R^-3 от центрального тела. Поэтому Луна, которая находится к Земле существенно ближе, несмотря на свою малую массу, создает приливную силу почти в 2 раза большую, чем Солнце.

   Каждое из этих светил создает во внешних оболочках Земли, прежде всего в океане, длинную приливную волну, два горба которой расположены на ближней и дальней сторонах Земли. Естественно, что лунный прилив движется по поверхности Земли вслед за движением Луны, а солнечный, вдвое меньший - за Солнцем. Во время полнолуний и новолуний, когда Луна и Солнце встают относительно Земли примерно на одну прямую, их приливные волны складываются, и наступает максимальный, т.н. "сизигийный" прилив; а когда они во время первой или последней четвертей Луны расходятся на небе на 90⁰, т.н. "квадратурные" или разностные приливы имеют минимальную высоту.

   Высота приливной волны в открытом море в тропической зоне (для бесконечного океана) составляет около 0.5 м, однако в реальных морях ее высота и форма определяется береговой линией и распределением глубин. Максимальные по высоте океанические приливы на Земле наблюдаются в заливе Фанди ( Северо-Западная Атлантика) - до 18 м. Приливы в земной коре, амплитуда которых составляет до 0.2 м, могут служить одним из "спусковых механизмов" для землетрясений.

   Типичные ошибки:
   - Луна притягивает к себе только легкую воду, а Солнце притягивает к себе всю Землю равномерно;

   Нетривиальные версии:
   - Потому что Луна - твердое тело, а Солнце - жидкое;
   - Потому что Солнце имеет высокую температуру, а Луна - низкую;
   - Луна принимает такие фазы, когда ее притяжение особенно сильно;
   - Ни лунных, ни солнечных приливов не существует, т.к. ни там, ни там нет воды;
   - Потому что приливы происходят в разное время суток, а сила притяжения в течение дня меняется;
   - Во время полнолуния люди становятся лунатиками (не все), поэтому лунные приливы сильнее;
   - Потому что Луна совершает только колебательные движения, не вращаясь вокруг своей оси;
   - Луна создает приливы непосредственно в океане, а сила притяжения Солнца идет на удержание Земли на орбите;
   
   

8. Вопрос: Наиболее красивые и удобные для обзора места в Москве ( Крылатское, Поклонная гора, Воробьевы горы, Коломенское) расположены на правом берегу Москвы-реки. Случайно ли это ?

   Ответ: Не случайно, поскольку правые берега рек сильнее размываются.

   Критерии оценки: Указан подмыв правого берега -1; Указано вращение Земли, как причина -1; Упомянуты закон Бэра или сила Кориолиса-1; Итого-3 балла.

   Комментарий: Образование рек и эволюция речных долин, безусловно, являются не случайными, а определяются такими общими факторами, как интенсивность и периодичность выпадения осадков в данном регионе, особенности рельефа местности и свойства подстилающих пород. Во-первых, очевидно, что воды, стекающие с площади водосбора, в целом движутся по уклону рельефа, который и определяет генеральное направление собирающей реки.

   Во-вторых, течение реки, встречая на своем пути локальные препятствия, будет отклоняться ими в ту или иную стороны, создавая повороты речного русла. В силу инерции движущейся воды на каждом таком повороте верхний, более быстрый слой будет отбрасываться к внешнему берегу, а придонный - к внутреннему. Создающееся при этом водоворотное течение будет интенсивнее подмывать внешний берег, переносить взятый материал и откладывать его на внутреннем берегу реки. За счет этого механизма внешний берег на повороте речного русла будет постоянно отступать, а любые изгибы реки, сответственно, увеличиваться. Эта принципиальная неустойчивость русла и способность рек к развитию своих изгибов и петель называется "меандрированием" по реке Меандр в Малой Азии.

   Замечено также, что все реки интенсивнее подмывают свой правый (по течению) берег, так что речные долины с течением времени смещаются вправо. Это явление получило название закона Бэра. Впоследствии было установлено, что в южном полушарии Земли реки подмывают свой левый берег. Это объясняется действием силы инерции в неинерциальной, вращающейся системе координат (Земля), которая называется силой Кориолиса. Она отклоняет любое движущееся тело вправо в северном полушарии и влево - в южном. Ее величина пропорциональна скорости движения и синусу широты места. Соответственно, в Евразии все реки "прижаты" в своих руслах к возвышенностям на правом краю речных долин. (Контрпример: Боровицкий холм Кремля - на левом берегу Москвы-реки).

   Типичные ошибки:
   - Потому что на правом берегу местность более холмистая;
   - Т.к. Москва стоит на 7-ми холмах;
   - Люди изначально начали селиться на правом берегу;
   - Это предосторожность от затопления;

   Нетривиальные версии:
   - Эти места специально выбрал Юрий Долгорукий;
   - Потому что с левой стороны часто нападали иностранцы;
   - Слева были набеги недругов, а справа мы от них защищались;
   - Правые берега выше левых, особенно в нашей стране;
   - Поверхность России в целом наклонена на север;
   - Не случайно, т.к. если один берег поднимается, то другой - опускается;
   - На правом берегу солнце больше освещает землю, чем на левом;
   - На правом берегу Москвы-реки более плодородная почва;
   - Река имеет большее влияние на правый берег;
   - Раньше река разливалась на правый берег, вымывая красивые места;
   - Литосферные плиты активнее двигались у правого берега, и строение земной коры там более гористое;
   - Правый берег выше из-за прошедшего там ледника;
   - Не случайно, потому что хотели более лучше украсить правый берег;
   - На правом берегу Москвы-реки наступает рассвет;
   
   

9. Вопрос: Известно, что можно определять стороны света по часовой стрелке. Каким образом это можно сделать, находясь в Эфиопии ? А в Новой Зеландии ?

   Ответ: В наших широтах половина угла между 12 и часовой стрелкой, направленной на Солнце, показывает юг, в Новой Зеландии - между 12, направленой на Солнце, и часовой стрелкой - север, а в Эфиопии этот метод не действует.

   Критерии оценки: Правильно описан метод часовой стрелки -1 балл; Указано вертикальное положение на экваторе -1; Указано обратное движение Солнца над севером для Южного полушария -1; Итого- 3 балла.

   Комментарий: Обычный метод определения сторон света по Солнцу и часовой стрелке, как известно, состоит в следующем: часовая стрелка на циферблате направляется на Солнце, угол между ней и цифрой 12 делится пополам, и эта линия и есть направление на юг (для декретного времени берется цифра 1, для летнего декретного - 2 ). Этот метод дает приемлемую для ориентирования на местности ошибку до 30 ⁰ в северных широтах (выше 50 ⁰ ), где Солнце можно предполагать движущимся вдоль южной части гризонта слева направо с угловой скоростью, вдвое меньшей, чем угловая скорость часовой стрелки, и находящимся над точкой юга приблизительно в 12 часов среднего солнечного времени, или в 13 часов декретного, или в 14 часов декретного летнего времени.

   В экваториальной части Земли (например, в Эфиопии) Солнце на небе движется почти перпендикулярно линии горизонта, проходя около полудня недалеко от зенита. Очевидно, что ориентирование по Солнцу и часам в это время практически невозможно. В утренние часы, от 6 до 9 часов, Солнце поднимается на восточной стороне горизонта, а в вечерние - с 15 до 18, - опускается на западной.

   В южном полушарии Земли Солнце движется вдоль северной стороны горизонта справа налево, в обратную сторону относительно часовой стрелки. Данный метод также можно применять в высоких южных широтах (например, в Новой Зеландии), только на Солнце нужно направить цифру 12 на часах ( или 1, или 2, соответственно), а не стрелку, и полученное направление биссектрисы угла между Солнцем и стрелкой будет показывать направление на север, а не на юг.

   Типичные ошибки:
   - Направление на юг можно определить только в полдень;
   - Можно ориентироваться по часовым поясам;

   Нетривиальные версии :
   - Не знаю, ни там, ни там не был;
   - В Новой Зеландии все наоборот;
   - Эфиопия и Новая Зеландия находятся в других часовых поясах, и там узнать стороны света нельзя;
   - Солнце быстро или медленно, но все-таки двигается на запад;
   - Часовую стрелку будет заклинивать, а вот как - не знаю;
   - Если поставить стрелки часов на нужное время, то определить стороны света можно;
   - Часовую стрелку отклоняет на север;
   - Если положить часы и подождать, пока они остановятся, то часовая стрелка будет показывать на ближайший магнитный полюс; в Эфиопии ближайший магнитный полюс - северный, и стрелка покажет на север; в Новой Зеландии - южный, и стрелка покажет на юг;
   - В северном полушарии вода в ванной спускается по часовой стрелке, а в южном - против часовой стрелки;
   
   

10. Вопрос: Смогут ли жители лунных поселений наблюдать корону Солнца во время затмений ?

    Ответ: Не смогут.

    Критерии оценки: Нет -1 балл; Указаны значительно большие размеры Земли -1; Указано преломление света в земной атмосфере -1; Указана возможность наблюдения короны при заходе Солнца -1; Итого- 4 балла.

    Комментарий: Прежде всего целесообразно напомнить, что на Земле корону Солнца нельзя видеть в любое время из-за рассеянного в земной атмосфере света вокруг солнечного диска, поскольку излучение короны в миллион раз слабее, чем самого Солнца. Во время полного солнечного затмения, когда Луна полностью закрывает диск Солнца, а размеры пятна лунной тени на поверхности Земли достигают нескольких сотен километров, яркость земного неба в центре полосы затмения может уменьшаться до 10 ^-9 от яркости Солнца, и корона на этом фоне становится видимой.

    На Луне, как известно, атмосферы нет, нет и рассеяния света. Однако, в обычных условиях, без затмений, прилегающая к диску Солнца корона не будет видна из-за слишком большого перепада яркости ( в 10 ⁶ раз). Единственным небесным телом, способным для лунного наблюдателя затмить Солнце, является Земля. Однако, размеры Земли в 3.7 раз больше, чем размеры Луны, соответственно, на лунном небе она будет занимать во столько же раз больше места, чем Луна на земном небе, и закроет не только само Солнце, но и солнечную корону тоже.

    Кроме этого, во время солнечного затмения на Луне свет от Солнца преломляется в земной атмосфере и заходит внутрь конуса геометрической тени. Этот преломленный солнечный свет для земного наблюдателя, который в это время наблюдает лунное затмение, создает т.н. "пепельный" или "багровый" цвет Луны, а для лунного наблюдателя образует вокруг тела Земли ярко светящийся ободок земной атмосферы, который также полностью перекрывает свечение солнечной короны.

    Единственным случаем, когда с поверхности Луны можно увидеть солнечную корону, являются лунные восходы и заходы Солнца, которые на Луне происходят через полмесяца. Но и при этом, когда диск Солнца находится непосредственно под горизонтом Луны, над ним можно видеть только часть солнечной короны. Таким образом, естественным путем с поверхности Луны никогда нельзя увидеть солнечную корону полностью.

    В качестве же самого простого искусственного метода ее наблюдения можно предложить закрыть диск Солнца пальцем или каким-нибудь иным, специально приспособленным для этой цели диском.

    Типичные ошибки:
    - Нет, т.к. на Луне пока никто не живет;
    Нетривиальные версии:
    - Смогут, т.к. Земля гораздо меньше Солнца;
    - И мы бы не увидели корону Луны, если бы Луна стала Солнцем;
    - Луна так расположена, что свет не может достичь Луны;
    - Смогут, т.к. корона - это солнечные лучи, а они очень длинные;
    - Не смогут, т.к. им будут мешать другие планеты;
    - Не смогут, т.к. корона образуется над ними и будет им слепить глаза;
    - Корона отражается от атмосферы Земли, поэтому на Земле она видна; на Луне нет атмосферы, - и корона там не видна;
    - На Луне свой календарь затмений;

Задачи конкурса по химии

Участникам турнира предлагается решить три из предложенных задач по собственному выбору (желательно, но не обязательно, решать задачи, предназначенные для соответствующего или более старшего класса)

Задача 1. (7-8 класс) Имеется смесь порошков поваренной соли, песка, серы и железа. Предложите способ разделения этой смеси, который позволит выделить каждое вещество в индивидуальном виде.

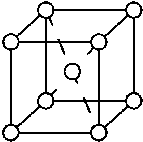
Задача 2. (7-8 класс) Металлическое железо образует объемноцентрированную кубическую решетку, одна ячейка которой изображена на рисунке (один атом в центре куба и восемь атомов в вершинах куба). Расстояние между центром и вершиной куба 0,247 нм (1 нм = 10^-9 м). Масса атома железа 9,03*10^-23 г. Рассчитайте плотность металлического железа.

Задача 3. (7-8) Горячий раствор нитрата натрия массой 400 г с массовой долей растворенного вещества 39% охладили до комнатной температуры. При этом часть вещества выпала в осадок, и его массовая доля в растворе составила 25%. Какова масса раствора после охлаждения?

Задача 4. (8-9 класс) Ангидридом кислоты называется кислотный оксид, который при взимодействии с водой может образовать соответствующую кислоту. Например, ангидридом серной кислоты является оксид SO₃ (SO₃ + H₂O = H₂SO₄). Каковы химические формулы ангидридов хлорной кислоты HClO₄, фосфорной кислоты H₃PO₄, угольной кислоты H₂CO₃? Напишите реакции этих оксидов с водой.

Задача 5. (8-10 класс) Юному химику потребовалось определить плотность маленького кусочка (крупинки) полимера. Он решил эту задачу, используя воду, поваренную соль и технические весы, которые имелись в школьной химической лаборатории. Как он это сделал? Всегда ли этот способ пригоден для определения плотности вещества?

Задача 6. (9-10 класс) Медную пластинку массой 50 г опустили на некоторое время в раствор нитрата ртути(II). Масса медной пластинки после промывания и высушивания увеличилась на 4,11 г. Затем пластинку нагревали до тех пор, пока она не приняла первоначальный цвет. Чему равна масса пластинки после нагревания?

Задача 7. (9-11 класс) Для восстановления 3,2 г оксида некоторого металла потребовалось 1.344 л водорода. При растворении полученного металла в избытке соляной кислоты выделилось 0,896 л водорода. Определите, какой это металл, напишите уравнения реакций.

Задача 8. (11 класс) Представьте себе некоторое количество метана (CH₄), в котором 50% атомов углерода представлено его изотопом ¹³C (остальное - ¹²C), а 50% атомов водорода - это его изотоп дейтерий D (²H). Изотопы статистичеки распределены по возможным положениям. Рассчитайте долю молекул метана с молекулярной массой 21.

Задача 9. (10-11 класс) Газообразный тритий (изотоп водорода ³H) подвергается радиоактивному распаду с образованием газообразного гелия согласно следующему уравнению:
T₂ -> 2³He + b
(b-частица представляет собой электрон). Определите, во сколько раз изменится давление в сосуде по истечении двух периодов полураспада трития (периодом полураспада называется время, за которое распадается половина имеющегося радиоактивного вещества).

Задача 10. (10-11 класс) 3 мл смеси газообразного углеводорода и 25 мл кислорода прореагировали в закрытом сосуде. После конденсации полученного водяного пара объем газообразного остатка был равен 19 мл, а после обработки щелочью осталось 7 мл газа. Установите формулу углеводорода, учитывая, что все измерения проводились при одинаковых условиях.

Краткие решения задач конкурса по химии

Задача 1.

1. Для начала смесь нужно поместить в воду. При этом соль растворится, а все остальное - нет. Сера всплывет, ее нужно аккуратно собрать, промыть водой и высушить.
2. Раствор отфильтровать. Фильтрат выпарить досуха, и полученную при этом соль высушить.
3. На фильтре останется смесь железа и песка. В принципе, если смесь высушить и высыпать на бумажку, железо можно отделить магнитом.

Задача 2. Плотность вещества - это отношение массы к объему. Таким образом, нужно найти объем ячейки и массу ячейки. Объем ячейки - это объем куба a³.
Большая диагональ куба 2*0,247*10^-9 м = 4,94*10^-10 м
Сторона куба a = d/(3^-1/2) (это легко найти по теореме Пифагора) = 2,85*10^-10 м.
Объем куба a³ = 2,315*10^-29 м³ = 2,315*10^-23 см³.
Число атомов железа в ячейке = 1 (в центре) + 1/8 *8 (в вершинах) = 2.
Масса 2*9,03*10^-23 г = 1,803*10^-22 г.
Плотность 1,803*10^{-22 г} / 2,31510^-23 см³ = 7,79 г/см³.

Задача 3.
Исходный раствор содержит 400*0,39 = 156 г вещества.
Пусть x г вещества выпало в осадок.
Осталось (156 - x) г.
Масса раствора после охлаждения (400 - x) г.
Составим уравнение:
(156 - x) / (400 - x) = 0,25
x = 74,67
400 - x = 325,33 (г).

Задача 4.
Cl₂O₇ + H₂O = 2 HClO₄ ;
P₂O₅ + H₂O = H₃PO₄ ;
CO₂ + H₂O = H₂CO₃.

Задача 5. Он положил крупинку полимера в воду и затем стал добавлять туда поваренную соль. В какой-то момент крупинка всплыла в объем раствора. Значит плотность раствора сравнялась с плотностью полимера. Затем юный химик определил плотность раствора соли. Так как у него не было справочника, чтобы узнать плотность раствора по ее концентрации, то он мог просто взвесить колбу с раствором, а затем взвесить ту же самую колбу с водой. Так как плотность чистой воды известна (1 г/см³), то отношение этих величин даст плотность раствора соли.

Такой способ применим, если искомая плотность вещества не больше плотности насыщенного раствора соли и если вещество никак не взаимодействует с водой (не набухает, не растворяется).

Задача 6.
Cu + Hg²⁺ = Cu²⁺ + Hg
Cu M_R = 64; Hg M_R = 201
Dm = 201 - 64 = 137 при растворении 1 моль меди. По условию масса увеличилась на 4,11 г. Значит растворилось 4,11/137 = 0,03 моля меди.
При нагревании пластинки, ртуть испарилась, осталась только медь.
0,03*64 = 1,92 г меди перешло в раствор. Осталось 50 - 1,92 = 48,08 г. Это и есть масса пластинки после нагревания.

Задача 7. Количество водорода, которое пошло на восстановление, не равно количеству, выделившемуся при растворени в кислоте, так как металл имеет разную степень окисления в исходном оксиде и в хлориде. Отношение 1,344 / 0,896 = 3/2. Значит, соответствующие степени окисления 3 и 2. Определим металл.
M₂O₃ + 3 H₂ = 2 M + 3 H₂O
1,344 / 22,4 = 0,06 моль
Оксида металла было 0,02 моль. 3,2 / 0,02 = 160
160 - 48 = 112. Молярная масса металла - 56. Это железо.

Задача 8.

Молекулярная масса 21 означает, что все атомы H и атом C замещены тяжелыми изотопами. Так как вероятность замещения каждого атома составляет 1/2, то вероятность замещения пяти атомов составляет (1/2)*5 = 1/32

Задача 9.

Пусть N исходное число молекул трития. При распаде образуется 2N молекул газа. За один период пулураспада распадается N/2 молекул и получается
N/2*2 = N
Всего в смеси находится N/2 + N молекул
После второго периода полураспада снова распадается половина имеющегося трития, т.е. N/4. Остается N/4 молекул трития. Получается N/2 молекул гелия.
Общее число молекул в смеси N/4 + N + N/2 = 7/4 N.
Давление увеличилось в 7/4 раза. (Период полураспада трития 12,33 года, поэтому можно считать, что температура постоянна).

Задача 10. Оставшиеся 7 мл газа - это избыток кислорода. Таким образом, в реакцию вступило 18 мл кислорода и получилось 12 мл CO₂.
C_xH_y + (x + y/4) O₂ = xCO₂ + y/2 H₂O
При сгорании 3 мл углеводорода получено 12 мл углекислого газа. Значит x = 4.
x + y/4 = 18/3 = 6
y/4 = 6 - 4 = 2; y = 8.
C₄H₈.

Вопросы и задания конкурса по истории

1. Юбилеи каких замечательных событий (кратные 100 годам) можно отметить в 1998 году?
2. В 17-18 веках в Европе возникли 4 прославленные академии наук. Где и когда они возникли? Кто из известных математиков стал первым членом двух из этих академий? Кто стал первым членом трёх из них? Кто - первым членом всех четырёх академий?
3. Укажите связи между научными открытиями Михаила Ломоносова и Джемса Кука. Составьте цепочку из общих знакомых между ними.
4. Перечислите 7 самых важных событий или процессов, происходивших в 19 веке.
5. Составьте перечень известных деятелей, знакомых с Сергием Радонежским. Кто из них был его другом, врагом, коллегой, учеником, соперником? Какие дела объединяли или сталкивали их между собой?
6. Перечислите известных вам деятелей Конкисты. Кто из них чем прославился?
7. Укажите государственных деятелей из других стран и времен, подобных Ивану Калите. Что общего в задачах, которые они решали, и в результатах их деятельности?
8. Составьте откровенный отзыв Сталина о Гитлере (или наоборот) - с указанием точной даты, когда составлялся этот отзыв.
9. Чем прославлены в археологии и в истории следующие места: Богазкей, Буреть, Гиссарлык, Гнездово, Дзибильчальтун, Каракорум, Кармир-блур, Мальта, Мохенджо-даро, Навкратис, Ниса, Накш-и-Рустам, Сунгирь, Тель-эль-Амарна, Тилля-тепе, Толстая могила, Хараппа, Чаталь-гююк, Чжоукоудянь?
10. Назовите имена ученых, впервые расшифровавших древнейшие письменности разных народов Земли.
11. Найдите в тексте историчекские ошибки.

АРХИМЕД (текст с ошибками)

Утро мартовских ид 105 года эры Александра не предвещало ничего замечательного. Как обычно, в Остии - порту Сиракуз - шла разгрузка очередных караванов. Скифы привезли на продажу понтийскую пшеницу, а египтяне - рис, который они научились выращивать у индийцев, покоренных великим Александром. На одном из египетских кораблей прибыл дорогой гость - Эратосфен, старый друг Архимеда, ставший директором Александрийского Музея.

Десять лет друзья не виделись - лишь обменивались письмами, сообщая о самых свежих научных открытиях. И вот пришла пора сравнить результаты двух ведущих школ греческого мира: Александрийского Ликея и Сиракузской Академии. Эратосфена сопровождает весь цвет ученой молодежи Египта: Конон, Герон, Диофант и другие, пока известные в Сиракузах только по именам. Конечно, прежде всего разговор пойдет о геометрии. Александрийцы пришли в восторг от теоремы Архимеда об объеме шара и хотят, чтобы автор изложил во всех подробностях свой "метод песчинок" - неожиданную смесь геометрии с арифметикой, которая обещает еще более ценные плоды.

Если Архимеда именуют "царем геометров", то Эратосфен - король старой арифметики и новой алгебры. Он сумел сделать то, что не удалось великому Пифагору: нашел 311 целочисленных прямоугольных треугольников и доказал, что других не бывает!

Заодно Эратосфен увлекся простыми числами, на которых, по мнению Пифагора, держится весь мир. Он доказал, что их множество бесконечно, а теперь ищет общую формулу простого числа. В этих поисках Эратосфен столкнулся с "близнецами" - парами и тройками простых чисел, стоящими подряд. Очень важно понять: конечно их множество, или нет ? Если оно бесконечно, то никакая формула-многочлен не может задать все простые числа! Значит, придется изобрести какие-то новые функции, которые стремятся к бесконечности не монотонно, а как бы по ступенькам... Тут есть о чем подумать лучшим математикам Средиземноморья!

Но не одной математикой увлекаются ученые мужи Александрии. Есть еще химия: древнее искусство египтян превращать одни вещества в другие. Конечно, всякий металлург может назвать себя химиком - раз он выплавляет из руд медь или платину. Но превратить тела моллюсков в алую краску, или обычное вино - в горючую жидкость - это под силу только мастерам древней страны Кемт и их греческим ученикам! Возможно, этот путь поможет описать все множество природных стихий - от всем понятной воды до загадочного апейрона, который безуспешно искали Пифагор и Евклид.

Недавно Архимеда поседила неожиданная мысль на этот счет. Известно, что любой металл (кроме золота) можно испортить, погрузив в уксус. И напротив - металлург наполняет печь углем, который отнимает порчу у руды, превращая ее в металл. Не значит ли это, что все камни суть металлы, испорченные уксусом и другими кислотами ? Надо только научиться возвращать металлам их благородный блеск, нагревая в жарком пламени! Пример тому - Солнце, которое жарче всего на свете и потому состоит из золота. С тех пор, как Аристарх доказал, что Солнце стоит в центре мироздания, каждому мудрецу ясно: все планеты произошли от Солнца, а все вещества - из солнечного золота, путем его порчи при охлаждении. Значит, в каждом камне таится золото! Порою оно проглядывет в форме блеска, или сверкает искрами при ударе камня о камень...

Все эти догадки надо обсудить с Эратосфеном. Если они верны и если удастся выделить в чистом виде ту стихию, которая способна испортить даже золото - тогда химия станет столь же точной наукой, как арифметика, а стихии будут играть в ней роль простых чисел! Уж тогда мы узнаем форму атомов разных стихий: сбудется вековая мечта Платона!

Увы, большая часть этих ученых надежд не сбылась, ибо научную встречу эллинов в Сиракузах оборвали боевые действия. Римский флот под командой Аттилия Регула осадил Сиракузы с требованием, чтобы царь Дионисий встал на сторону Рима в его борьбе с Ганнибалом. Уничтожив при Каннах римскую армию Сципиона, свирепый фождь финикийцев осадил Рим - и теперь римляне пытались отрезать Ганнибала от подкреплений, которые шли к нему из Африки через Сицилию. Так невезучий остров вновь стал ареной войны между чужеземными армиями.

Правнук великого Александра - царь Филипп, занятый войною с грозным Пирром, не успел помочь грекам Сицилии в их беде. В конечном счете финикийская армия была уничтожена молодым римским полководцем Серторием. Повторно осадив Сиракузы, он потребовал выкуп за гибель невезучего Аттилия Регула. Пусть славный Архимед со всеми учениками переселится в Рим, подобно Евклиду - иначе Сиракузы будут разрушены, а всех жителей ожидает рабство!

Старый патриот Архимед хотел покончить с собою - но сограждане упросили его пожертвовать своей честью ради их счастья. Так греческая ученость вынужденно перенеслась из Сицилии в Рим. Став не только сильнейшим, но и ученейшим городом Италии, Рим сделал последний решающий шаг на пути к мировому господству. Славная Александрия хранила свою независимость в течение еще одного поколения - до кончины Эратосфена; затем ее постигла судьба Сиракуз. В результате внук Эратосфена - Полибий - сделался римским ученым. Он написал историю войн римлян за сплочение Средиземноморья в нерушимую империю, которая процветала в течение семи веков.

Решения задач конкурса по истории

В турнире участвовало около 2200 школьников, из них в конкурсе по истории - 284 человека. В их числе 15 удостоены премий, 47 - похвальных отзывов, еще 67 - условных отзывов, которые выдаются, если участник сделал что-то заметное ещё и по другим наукам. Таким образом, почти половина участников конкурса сделала нечто стоящее - либо за счет эрудиции, либо (реже) за счет качества научного мышления.

Не удивительно, что все премии достались ученикам известных гимназий и лицеев: 57, 91, 325, 444, 1199, 1201, 1508, 1510, 1543, 1567. Приятно, что среди лауреатов 98 года есть ветераны прошлого года - но еще приятнее, что большинство нынешних лауреатов впервые изведали вкус премии. Значит, контингент турнира Ломоносова в каждом году - только вершина айсберга, а всего в Москве наберется в 5-10 раз большее число активных и смышленых школьников. Труднее понять, почему в этом году треть премий досталась ученикам одной школы N57: в прошлые годы конкуренция среди гимназий была острее и интереснее. Не сыграл ли особую роль тот факт, что школа N57 устроила у себя вечерний кружок, открытый для будущих гуманитариев со всей Москвы? Спасибо учителям истории, которые наладили это дело: С.И.Каспе, Б.М.Меерсону, А.И.Петроковскому!

1. Юбилеи каких замечательных событий (кратные 100 годам) можно отметить в 1998 году ?
   

   1898	первый съезд РСДРП в Минске
   1798	египетский поход Бонапарта
   1698	возвращение Петра из Европы; стрелецкая казнь
   1598	Борис Годунов взошел на трон
   1498	Васко да Гама достиг Индии
   1398	Тимур завоевал Индию
   1198	Иннокентий 3 стал римским папой
   898	мадьяры переселились в Венгрию
   498	Хлодвиг принял крещение
   98	Траян стал императором
   -202	Сципион победил Ганнибала при Заме

   
   

   В ответах школьников отразилось немалое разнообразие их исторических вкусов. Например, 1898 год связывали со съездом РСДРП, со введением золотого стандарта рубля, даже с юбилеем Набокова! 1798 год был связан не только с египетским походом Бонапарта, но и с экспедицией Ушакова в Ионию. Похвальная широта кругозора! Характерно, что 1698 год многие школьники связали с возвращением Петра из Великого посольства, меньшее число - с последним стрелецким бунтом, но никто - со Стрелецкой казнью. Можно похвалить столь явную неохоту подчеркивать людоедские детали российской и зарубежной истории!
   

   Дата (1598) не вызвала разногласий: либо конец династии Рюриковичей, либо восшествие на трон Бориса Годунова. Увы - никто не вспомнил Нантский эдикт Генриха 4! Иное дело - 1498 год: тут многие назвали третье путешествие Колумба, но почти никто не вспомнил достижение Индии Васко да Гамой. К сожалению, заморские успехи испанцев заслоняют во мнении российских школьников сходные достижения португальцев...
   

   Средневековые даты образуют зияющий провал. Никто не вспомнил крещение Хлодвига (498), переселение мадьяр в Венгрию (898) или восшествие Иннокентия 3 на папский трон (1198). Зато крещение Руси многие школьники охотно сдвинули на 10 лет вперед - ради круглой даты!
   

   Приятно отметить, что несколько школьников вспомнили две античные даты: последнюю битву Ганнибала при Заме (-202 год) и восшествие Траяна на имперский трон (98 год). Все же античная история помнится даже через много лет после ее изучения!
   
   

2. В 17-18 веках в Европе возникли 4 прославленные академии наук.
   Где и когда они возникли ?
   Кто из известных математиков стал первым членом двух из этих академий?
   Кто стал первым членом трёх из них?
   Кто - первым членом всех четырёх академий?
   
   А. Королевское Общество в Лондоне (1662 год)
   Б. Парижская Академия Наук (1666 год)
   В. Прусская Академия Наук в Берлине (1700 год)
   Г. Российская Академия Наук (1725 год)
   
   Первый член (А) и (Б), президент (Б) - Христиан Гюйгенс
   Первый член (А), (Б) и (В), президент (В) - Готфрид Лейбниц
   Первый член (А), (Б), (В) и (Г) - Даниил Бернулли
   

   Более 15 участников турнира верно назвали 4 академии: Но верно угадать все три персоны ученых не сумел никто - хотя было немало удачных догадок. Ближе всех к истине оказался Петр Попов из 1508 гимназии: он предложил Ньютона, Лейбница и Эйлера.
   

   Лейбниц угадан верно: он в 1700 году стал первым президентом Берлинской академии, уже будучи членом Лондонского Общества и Парижской Академии. Но Ньютон не был первым членом двух академий: его опередил его старший друг Гюйгенс, который был в числе членов-учредителей Королевского Общества и стал первым президентом Парижской Академии. Аналогично, Эйлера опередил его старший друг - Даниил Бернулли. Он приехал в Россию одновременно с Эйлером, но покинул ее раньше - и потому раньше удостоился на западе всех возможных научных почестей.
   
   

3. Укажите связи между научными открытиями Михаила Ломоносова и Джемса Кука. Составьте цепочку из общих знакомых между ними.
   

   Ломоносов разработал программу исследования полярных морей и прохождения Северного морского пути вокруг Азии.

   1. Кук первый обошел Южный полюс в полярных широтах (не достигнув Антарктиды) и пытался проникнуть в Северный Ледовитый океан через Берингов пролив - с целью обогнуть Америку с севера.

   Кроме этого, Ломоносов (в 1761 году) и Кук (в 1767 году) наблюдали прохождение Венеры по диску Солнца.
   

   2. Цепь знакомых: Ломоносов - Екатерина 2 - Дидро - Банкс(натуралист на судне Кука "Endeavor") - Кук.
   

   Первое задание никто не выполнил целиком - хотя многие вспомнили ломоносовский проект освоения Сибири через Северный Морской Путь вокруг Евразии. Но немногие школьники помнят о втором путешествии Кука - вокруг Антарктиды (которую он не сумел увидеть с дальних подступов), и никто не знает инструкцию Адмиралтейства к третьему путешествию: отыскать морской путь вокруг северного побережья Америки! Это поручение не было выполнено: сначала льды помешали Куку войти в Берингов пролив, а потом он был убит на Гавайях.
   

   Ни один школьник не вспомнил о прохождении Венеры по диску Солнца: в 1761 году Ломоносов наблюдал это явление из Петербурга, а в 1768 году Кук повторял наблюдение в Тихом океане. Увы - астрономия остается самой пренебрегаемой ветвью физики в нашей школе! Текст об Архимеде (см. ниже) выявил массовое незнание школьниками того факта, что гелиоцентрическую систему Вселенной впервые выдвинул Аристарх, а не Коперник.
   

   Что касается цепи из общих знакомых между Ломоносовым и Куком, то многие школьники предложили схему: Кук - король Георг 3 - английский посол в Петербурге - Екатерина 2 - Ломоносов. Есть и иная возможность: Ломоносов - Екатерина 2 - Дидро - Банкс - Кук. Дело в том, что натуралист Банкс (спутник Кука в первом путешествии) был знаком с великим просветителем, который посетил Россию после завершения своей Энциклопедии (и после смерти Ломоносова).
   
   

4. Перечислите 7 самых важных событий или процессов, происходивших в 19 веке.
   
   • Рождение и гибель империи Наполеона
   • Освобождение Латинской Америки от власти Испании
   • Война между Севером и Югом в США
   • Реформы Александра 2 в России
   • Объединение Германии Бисмарком
   • Реформа Мэйдзи в Японии
   • Развитие электроэнергетики и электросвязи
   
   

   Здесь испытанию подверглась не столько эрудиция школьников, сколько их научный вкус. Большинство ответов включало минимум очевидно важных событий: Наполеоновские войны, объединение Германии, освобождение крестьян в России, войну между Севером и Югом в США, промышленный переворот в Англии. Сверх этого, многие школьники предложили оригинальные новинки мирового значения: изобретение электросвязи (телеграф - телефон - радио), расцвет русской литературы (спасибо Пушкину и его близкому юбилею!), а также рождение египтологии, революционную деятельность Гаусса в математике и Фарадея - в физике. Как видно, участники турнира Ломоносова - действительно рыцари многих качеств, ценящие культуру и науку не ниже политических успехов!
   
   

5. Составьте перечень известных деятелей, знакомых с Сергием Радонежским. Кто из них был его другом, врагом, коллегой, учеником, соперником? Какие дела объединяли или сталкивали их между собой ?
   
   Партнеры Сергия в церкви:
   • игумен Стефан (брат, коллега и соперник);
   • митрополит Алексий (начальник и друг);
   • епископ Дионисий Нижегородский (коллега и соперник);
   • Федор Симоновский, Андроник и Стефан Пермский (ученики-игумены);
   • патриарх Филофей Коккин, игумен Григорий Палама (союзники в Византии);
   • протопоп Митяй (враг);
   • митрополит Киприан (союзник, но не друг);
   • Епифаний (ученик и биограф);
   • Андрей Рублев (ученик).
   
   

   К сожалению, абсолютное большинство школьников смогло назвать только Дмитрия Донского - иногда с добавлением Пересвета и Осляби. Но нашлось немало приятных исключений, которые трудно объяснить. Так, более 10 школьников назвали Стефана - брата Сергия, указав, что тот был его соперником на посту игумена Троицы. Несколько человек назвали ученика и биографа Сергия - Епифания Премудрого. Из других учеников называли Стефана Пермского, Андроника, Андрея Рублева и даже Федора Симоновского - с указанием, что тот был племянником Сергия! Видно, что многие московские учителя истории считают Сергия культурным героем первой величины, и не согласны с мнением на этот счет авторов массового учебника - Л.А.Кацвы и А.Л.Юрганова. Жаль, что те же учителя поскупились рассказать ученикам о митрополите Алексии: имя "русского Ришелье" назвали только 3 участника турнира, имя Дионисия Нижегородского - лишь один участник. А ведь многие учителя и родителя читают романы Д.М.Балашова!
   
   

6. Перечислите известных деятелей Конкисты. Кто из них чем прославился ?
   
   Принц Энрике и король Жоао 2: организаторы Конкисты в Португалии.
   Короли Фернандо Арагонский и Изабелла Кастильская: организаторы Конкисты в Испании.

   Христофор Колумб (открыл путь в Америку). Бартоломеу Диаш и Васко да Гама (открыли путь в Индию). Васко Нуньес де Бальбоа (первый пересек Америку и увидел Тихий океан). Фернандо Магеллан (первый пересек Тихий океан и открыл Филиппинские острова). Франсиско Орельяна (первым проплыл по Амазонке).

   Альфонсу Альбукерке (разгромил флоты мусульман в Индийском океане и открыл все гавани Индии для португальцев). Эрнандо Кортес (завоевал царство ацтеков в Мексике). Франциско Писарро (завоевал царство инков в Перу). Гонсало Кесада (завоевал царство муисков в Колумбии). Франциско Монтехо (покорил княжества майя на Юкатане).
   

   Очень многие школьники назвали Кортеса и Писарро, верно указав их завоевания. Третье место занял Бальбоа - открыватель Тихого Океана, четвертое - Магеллан, впервые пересекший его. Зато Орельяну на Амазонке вспомнили очень немногие - и лишь трое заметили, что Фердинанда и Изабеллу можно считать "заказчиками" Конкисты! К сожалению, никто не догадался присоединить к числу активных властителей императора Карла 5, португальского принца Энрике и короля Жоао 2. И никто не назвал отважных португальских капитанов: Бартоломеу Диаша, Васко да Гаму, Альфонсо Альбукерке - покорителя Индийского Океана.
   
   

7. Укажите государственных деятелей из других стран и времен, подобных Ивану Калите. Что общего в задачах, которые они решали, и в результатах их деятельности ?
   Иван Калита поднял Московское княжество из ничтожества к могуществу, сочетая мудрую умеренность в экономике и законодательстве с жесткой и хитрой политикой.
   В Англии сходную роль сыграли короли Генрих 2(в 12 веке) и Генрих 7 (в 16 веке).
   Во Франции - короли Филипп 2 Август (в 13 веке) и Луи 11 (в 15 веке).
   В Испании - короли Фернандо и Изабелла (15 век).
   В Германии - канцлеры Бисмарк (19 век), Аденауэр и Коль (20 век).
   

   При решении этой задачи эрудиция школьников была гораздо менее важна, чем культура их исторического мышления. Приятно отметить, что такой культурой обладают многие "незнайки", которых никак нельзя назвать невеждами. Хотя многие готовы уподобить Калите любых удачливых правителей, создавших великие державы (вплоть до Александра Македонского!) - но немало нашлось учеников, верно оценивших тихое и скрытное "собирательство" Калиты. На этом основании в ряд его аналогов встали первые консулы Римской Республики, а также Филипп 2 Македонский и Гиерон Сиракузский, который долго и успешно балансировал между Эпиром, Римом и Карфагеном.
   

   Из деятелей нового времени были по заслугам названы Фридрих Вильгельм Прусский (отец Фридриха 2), а также германские канцлеры: Бисмарк и Коль (к сожалению, никто не вспомнил хитрейшего Аденауэра). Из средневековых правителей с Калитою сравнивали Филиппа 2 Августа и Людовика 11 во Франции, Генриха 2 и Генриха 7 в Англии - тех, что поднимали свое отечество из разрухи гражданских войн.
   

   Но совсем неожиданным аналогом Калиты стала Клеопатра, которая долго и удачно стравливала Антония с Октавианом, чтобы помешать объединенному Риму поглотить ослабевший Египет. Пожалуй, сам Иван Данилович не возразил бы против такого уподобления своего диалога с ханами Орды!
   
   

8. Составьте откровенный отзыв Сталина о Гитлере (или наоборот) - с указанием точной даты, когда составлялся этот отзыв.
   
   К сожалению, немногие школьники сочинили умный и откровенный отзыв одного диктатора о другом - которого он одновременно ненавидит и уважает, готов учиться разным хитростям у своего партнера. За эту задачу взялись около 30 школьников: каждый десятый участник исторического конкурса. Две трети составили поверхностные отзывы, где автор только осуждает своего врага. Остальные выразили уважение или даже зависть Сталина к Гитлеру (которому судьба вручила столь послушный и умелый народ), либо Гитлера к Сталину (которому незачем воевать ради жизненного пространства). Прозвучала и мечта Сталина: как бы подольше мирно сосуществовать с умелым владыкой Германии, ради победы над враждебной им обоим Западной Европой! Но самый глубокий отзыв сочинила Наташа Синайская (1522 гимназия), датировав его 1950 годом.
   
   
9. Чем известны в археологии и в истории следующие места: Богазкей, Буреть, Гиссарлык, Гнездово, Дзибильчальтун, Каракорум, Кармир-блур, Мальта, Мохенджо-даро, Навкратис, Ниса, Накш-и-Рустам, Сунгирь, Тель-эль-Амарна, Тилля-тепе, Толстая Могила, Хараппа, Чаталь-гююк, Чжоукоудянь ?
   
   1. Чжоукоудянь - пещера в Китае, где тысячи лет обитали синантропы.
   2. Мальта, Буреть и Сунгирь - стоянки людей палеолита в Сибири и европейской России.
   3. Толстая Могила - группа скифских курганов с богатыми захоронениями.
   4. Чаталь-гююк - древнейший город в Малой Азии (еще без крепостной стены).
   5. Ниса - столица древней Парфии.
   6. Накш-и-Рустам - скальные гробницы персидских царей (Ахеменидов и Сасанидов).
   7. Тель-эль-Амарна - руины столицы фараона Эхнатона.
   8. Тилля-тепе - гробница царей-кочевников Кушан в Афганистане.
   9. Мохенджо-даро и Хараппа - древнейшие города Индии.
   10. Кармир-блур - руины урартской крепости Тейшебаини.
   11. Богазкей - руины столицы царства хеттов.
   12. Гиссарлык - холм с руинами Трои.
   13. Гнездово - древнейшее поселение и кладбище близ Смоленска.
   14. Каракорум - руины столицы Чингисхана.
   15. Навкратис - первая греческая колония в устье Нила.
   16. Дзибильчалтун - руины крупнейшего из городов майя на полуострове Юкатан.
   
   

   Очень многие школьники помнят, что холм Гиссарлык - это развалины Трои. Многие знают, что Каракорум - бывшая столица Чингисхана, а Мохенджо-даро и Хараппа - древнейшие города Индии. Но немногие вспомнили, что Тель-эль-Амарна - современное название руин столицы Эхнатона, а Навкратис - древнейшая колония эллинов в дельте Нила. Несколько человек вспомнили, что Ниса - столица древней Парфии (расположенная в Туркмении), а Чаталь-гююк - руины города в Анатолии, не имевшего стен и более древнего, чем Иерусалим. Очень немногие вспомнили или сообразили, что Толстая Могила - название одного из скифских курганов, а Богазкей - руины одной из хеттских столиц (в Турции). Один-два человека вспомнили имя пещеры Чжоукоудянь вблизи Пекина, как место обитания синантропов; но гораздо большее число школьников решило, что это - имя одной из столиц империи Хань.
   

   Многих школьников ввело в заблуждение знакомое имя острова: Мальта. Никто не знал, что так называется одна из палеолитических стоянок в Сибири, раскопанная (как и Буреть) А.Окладниковым. Но один из школьников удачно использовал сведения, почерпнутые из телепередачи "Вокруг Света": в ней говорилось, что на острове Мальта раскопаны неолитические поселения 5 тысячелетия до н.э.
   

   К сожалению, никто из школьников не опознал Сунгирь - ручей и стоянку палеолита близь города Владимира, где найдено захоронение двух мальчиков и вождя с богатым погребальным инвентарем (включая копье из распрямленного бивня мамонта). Также никто не опознал Тилля-тепе ("Золотой холм") - группу царских могил династии Кушан в Северном Афганистане, открытую и частично раскопанную В.И.Сарианиди накануне Афганской войны.
   

   Понятно, что никто из школьников не опознал имя заброшенного города майя: Дзибильчальтун. Труднее понять, почему ни один участник турнира не узнал Гнездово - городище вблизи Смоленска, излюбленное нашими археологами. Жаль также, что некрополь персидских царей Накш-и-Ростом остался не опознан ни одним из юных любителей исторической науки.
   
   

10. Назовите имена ученых, впервые расшифровавших древнейшие письменности разных народов Земли.
    
    1. Шампольон - прочел египетские иероглифы.
    2. Гротефенд - начал читать персидскую клинопись.
    3. Роулинсон - прочел полностью персидскую часть Бехистунской надписи Дария 1, и частично - ее эламский текст.
    4. Опперт, Толбот и Хинкс - вместе с Роулинсоном начали уверенно читать аккадскую клинопись.
    5. Вентрис - расшифровал линейное письмо "Б" на Крите.
    6. Грозный - прочел клинопись хеттов.
    7. Кнорозов - прочел рукописи майя.
    
    

    Конечно, большинство школьников назвало Франсуа Шампольона - хотя некоторые нарекли его Шатильоном или даже Шампиньоном. Более 10 участников назвали Г.Гротефенда, начавшего дешифровку персидской клинописи. 5 человек назвали Б.Грозного - дешифровщика клинописи хеттов - и Г.Роулинсона, котороый прочел весь персидский текст и часть эламского текста в Бехистунской надписи Дария 1. К сожалению, ни один школьник не вспомнил М.Вентриса, прочитавшего критское (греческое) линейное письмо "Б". Но два ученика назвали Ю.Кнорозова, прочитавшего рукописи майя. Наконец, один герой - Миша Вогман из 57 школы (который, как выяснилось, недавно сделал соответствующий доклад на школьном кружке) - вспомнил имена всех четырех участников экзамена 1851 года, когда виднейшие ассириологи (Роулинсон, Толбот, Опперт и Хинкс) переводили незнакомый аккадский текст. Чего только не знают юные гуманитарии нашего времени!

Комментарии к ошибкам в тексте "Архимед"

АРХИМЕД (текст с ошибками)

Утро мартовских² ид² 105 года эры Александра¹ не предвещало ничего замечательного. Как обычно, в Остии - порту Сиракуз³ - шла разгрузка очередных караванов. Скифы привезли⁴ на продажу⁶ понтийскую пшеницу, а египтяне - рис⁵, который они научились выращивать у индийцев⁵, покоренных великим Александром. На одном из египетских кораблей прибыл дорогой гость - Эратосфен, старый друг Архимеда, ставший директором Александрийского Музея.

Десять лет друзья не виделись⁷ - лишь обменивались письмами, сообщая о самых свежих научных открытиях. И вот пришла пора сравнить результаты двух ведущих школ греческого мира: Александрийского Ликея⁸ и Сиракузской Академии⁹. Эратосфена сопровождает весь цвет ученой молодежи Египта: Конон¹⁰, Герон¹¹, Диофант¹² и другие, пока известные в Сиракузах только по именам. Конечно, прежде всего разговор пойдет о геометрии. Александрийцы пришли в восторг от теоремы Архимеда об объеме шара и хотят, чтобы автор изложил во всех подробностях свой "метод песчинок" - неожиданную смесь геометрии с арифметикой, которая обещает еще более ценные плоды.

Если Архимеда именуют "царем геометров", то Эратосфен - король¹⁴ старой арифметики и новой алгебры¹³. Он сумел сделать то, что не удалось великому Пифагору: нашел 311 целочисленных прямоугольных треугольников и доказал, что других не бывает!¹⁵

Заодно Эратосфен увлекся простыми числами, на которых, по мнению Пифагора, держится весь мир. Он доказал, что их множество бесконечно¹⁶, а теперь ищет общую формулу простого числа¹⁷. В этих поисках Эратосфен столкнулся с "близнецами" - парами и тройками простых чисел, стоящими подряд¹⁸. Очень важно понять: конечно их множество, или нет? (см. комментарий¹⁹) Если оно бесконечно, то никакая формула-многочлен¹⁷ не может задать все простые числа! Значит, придется изобрести какие-то новые функции, которые стремятся к бесконечности²⁰ не монотонно, а как бы по ступенькам... Тут есть о чем подумать лучшим математикам Средиземноморья!

Но не одной математикой увлекаются ученые мужи Александрии. Есть еще химия: древнее искусство египтян²¹ превращать одни вещества в другие. Конечно, всякий металлург может назвать себя химиком - раз он выплавляет из руд²³ медь или платину²². Но превратить тела моллюсков в алую краску²⁵, или обычное вино - в горючую жидкость²⁴ - это под силу только мастерам древней страны Кемт и их греческим ученикам! Возможно, этот путь поможет описать все множество природных стихий²⁶ - от всем понятной воды до загадочного апейрона, который безуспешно искали Пифагор и Евклид²⁷.

Недавно Архимеда поседила неожиданная мысль на этот счет²⁸. Известно, что любой металл (кроме золота) можно испортить, погрузив в уксус. И напротив - металлург наполняет печь углем, который отнимает порчу у руды, превращая ее в металл. Не значит ли это, что все камни суть металлы, испорченные уксусом и другими кислотами?²⁹ Надо только научиться возвращать металлам их благородный блеск, нагревая в жарком пламени! Пример тому - Солнце, которое жарче всего на свете³⁰ и потому состоит из золота. С тех пор, как Аристарх доказал, что Солнце стоит в центре мироздания, каждому мудрецу ясно: все планеты произошли от Солнца³¹, а все вещества - из солнечного золота, путем его порчи при охлаждении. Значит, в каждом камне таится золото! Порою оно проглядывет в форме блеска, или сверкает искрами при ударе камня о камень...³²

Все эти догадки надо обсудить с Эратосфеном. Если они верны и если удастся выделить в чистом виде ту стихию, которая способна испортить даже золото - тогда химия станет столь же точной наукой, как арифметика, а стихии будут играть в ней роль простых чисел! Уж тогда мы узнаем форму атомов разных стихий: сбудется вековая мечта Платона!³³

Увы, большая часть этих ученых надежд не сбылась, ибо научную встречу эллинов в Сиракузах оборвали боевые действия. Римский флот под командой Аттилия Регула³⁴ осадил Сиракузы с требованием, чтобы царь Дионисий³⁶ встал на сторону Рима в его борьбе с Ганнибалом. Уничтожив при Каннах римскую армию Сципиона³⁸, свирепый фождь финикийцев осадил Рим³⁹ - и теперь римляне пытались отрезать Ганнибала от подкреплений, которые шли к нему из Африки³⁷ через Сицилию³⁷. Так невезучий остров вновь стал ареной войны между чужеземными армиями.

Правнук великого Александра - царь Филипп⁴⁰, занятый войною с грозным Пирром⁴¹, не успел помочь грекам Сицилии в их беде. В конечном счете финикийская армия была уничтожена молодым римским полководцем Серторием⁴². Повторно осадив Сиракузы, он потребовал выкуп за гибель невезучего Аттилия Регула³⁵. Пусть славный Архимед со всеми учениками переселится в Рим⁴³, подобно Евклиду⁴⁴ - иначе Сиракузы будут разрушены, а всех жителей ожидает рабство!

Старый патриот Архимед хотел покончить с собою - но сограждане упросили его пожертвовать своей честью ради их счастья. Так греческая ученость вынужденно перенеслась из Сицилии в Рим⁴⁵. Став не только сильнейшим, но и ученейшим городом Италии⁴⁶, Рим сделал последний решающий шаг на пути к мировому господству. Славная Александрия хранила свою независимость в течение еще одного поколения - до кончины Эратосфена; затем ее постигла судьба Сиракуз⁴⁷. В результате внук Эратосфена - Полибий⁴⁸ - сделался римским ученым. Он написал историю войн римлян за сплочение Средиземноморья в нерушимую империю, которая процветала в течение семи веков⁴⁹.

Как обычно, наибольший простор для ума или недомыслия школьников представил текст со вставленными историческими ошибками - на этот раз посвященный Архимеду. В нем политические несуразицы чередовались с нелепостями из истории науки. Начнем с обзора самых массовых заблуждений, проявленных школьниками на этом фронте.

А. Самая странная из иллюзий - будто частной переписки между учеными Средиземноморья не было, пока Рим не охватил этот регион своей властью и государственной почтовой службой. На деле культура обмена частных лиц письмами "с оказией" процветала в этом регионе еще в персидскую эпоху - и пышно расцвела в эллинистическом мире, когда греческий язык стал международным. Не случайно половина открытий Архимеда известна нам из его писем к друзьям в Александрию.

Б. Многие школьники догадались, что египтяне не выращивали рис в эпоху Архимеда - но дали этому факту неверное объяснение, будто рис тогда не рос даже в Индии, или что в Египте для него неподходящий климат. В действительности рис впервые был освоен в Индокитае и распространился в Китае и в Индии задолго до античной эпохи. Но на Ближний Восток эта трудоемкая культура проникла только в Средневековье - после того, как арабы подчинили Египет, Двуречье и часть Индии.

В. Почти все школьники не знают и не верят, что гелиоцентричную модель Вселенной впервые предложил Аристарх - и обосновал ее, приближенно рассчитав диаметр Солнца (он оказался больше диаметра Земли - а большой шар вряд ли может обращаться вокруг малого шара). Слишком сильно мы забили детские головы приоритетом Коперника - который превзошел Аристарха лишь в точности расчетов! Беда Аристарха в том, что его ученые современники (как и школьники наших дней) не верили расчетам, которые противоречат "здравому смыслу". К тому же схема Аристарха не позволила астрономам рассчитывать движение планет более точно, чем привычная схема Евдокса (с эпициклами).

Г. Многие школьники возмутились утверждением, будто Эратосфен и другие математики - "египетские" ученые: ведь они - греки (как видно из их имен), а Древний Египет был раньше Древней Греции! Увы: нынешняя система преподавания истории так уверенно и просто разложила всю Древность по полочкам, что для синтетических эпох (вроде эллинизма) не осталось места в детских умах. Не поможет ли этой беде сравнение Птолемеевского Египта с Послепетровской Россией, где при дворе также преобладали иностранные языки ?

Д. Очень многие школьники не поверили в наличие до^'менных печей в Античном мире. Это странно, и свидетельствует о плохой технической грамотности. Ведь только в домне, с поддувом воздуха, можно выделить из руды железо (в отличие от легкоплавкой меди) - а Железный век начался в Средиземноморье за тысячу лет до Архимеда! Если учитель физики не сообщил детям этот факт, то исправить эту ошибку должен историк.

Е. Странно, что слово "караван" почти все школьники восприняли, как "караван верблюдов". Неужели "караван судов" - незнакомое понятие даже для выпускников нашей школы? Видимо, это отражает убывающую популярность курса географии в школе - а "историк, не сведущий в географии, на каждом шагу встречает претыкание" - порою такое смешное, как "караван в гавани".

Ж. Ахиллесовой пятой абсолютного большинства школьников оказались (как следовало ожидать) даты жизни античных ученых. Эти даты никто не связывал с открытиями Пифагора, Евклида, Архимеда или Эратосфена - даже в математике, где логическая связь научных результатов позволяет без особого труда восстановить последовательность их появления. Оттого в работах школьников изобиловали бездоказательные утверждения о том, что "Архимед и Эратосфен жили в разные времена", или что "Пифагор жил после Архимеда". Очень многие ученики физматшкол ничего не слышали о "методе песчинок" Архимеда - первом варианте интегрального исчисления - и даже о том, что Архимед дал первое строгое доказательство формулы объема шара. Видно, что стык между историей науки и политической историей человечества остается не заполнен в учебном процессе даже ведущих московских гимназий. Напомним, что все приведенные ошибки взяты из лучших работ турнира, отмеченных премиями за то или иное проявление эрудиции либо культуры исторического мышления...

Приводим полный список "ошибок". Все номера пунктов оформлены в виде гиперссылок на соответствующие места текста с ошибками.

1. Александр Македонский начал править в 336 году до н.э. Значит, 105 год его эры - это 231 или 230 год до н.э. Но осада Сиракуз и гибель Архимеда - события 212 года до н.э.
2. Ни в каком греческом календаре не было римского месяца "март" или дня с названием "иды".
3. Остия - это порт города Рима, а не Сиракуз (которые сами стоят на берегу моря).
4. Скифы выращивали ячмень, рожь и пшеницу в Причерноморье - но они не плавали по морю, а продавали зерно греческим купцам.
5. Египтяне начали выращивать рис только после арабского завоевания (когда сами арабы переняли эту культуру в Индии).
6. Сицилия была производителем зерна - так что туда редко привозили зерно на продажу.
7. После возвращения из Александрии в Сиракузы Архимед не встречался с Эратосфеном, хотя они регулярно переписывались.
8. Школа "Ликей", основанная Аристотелем, находилась в Афинах, а не в Александрии.
9. Название "Академия" употреблялось только в Афинах - где Платон учил молодежь в роще, посвященной герою Академу.
10. Математик Конон был учителем Архимеда и Эратосфена - так что он старше их обоих.
11. Ученый-механик Герон жил в Александрии в 1 веке н.э. - намного позже Архимеда и Эратосфена.
12. Математик Диофант работал в Александрии в 3 веке н.э.
13. Слово "алгебра" появилось в 9 веке н.э. - в трудах арабских математиков.
14. Слово "король" появилось в Средние века - в связи с Карлом Мартеллом и Карлом Великим.
15. Существует бесконечное множество прямоугольных треугольников со взаимно простыми сторонами. Этот факт был известен еще Пифагору.
16. Бесконечность множества простых чисел доказал Евклид - примерно за сто лет до гибели Архимеда.
17. Понятия "формула" и "многочлен" появились в математике с рождением европейской алгебры - в конце 16 века. До той эпохи никто не мог искать "общую формулу простых чисел".
18. Эратосфен обнаружил много пар "близнецов" - простых чисел вида (р; р+2). Но аналогичная тройка простых чисел есть только одна: (3,5,7). Это было известно еще Евклиду.
19. Вопрос о конечности или бесконечности множества "простых близнецов", несомненно, волновал Эратосфена. Но решить эту проблему не удалось до сих пор.
20. "Функции, стремящиеся к бесконечности" - такое выражение появилось в науке лишь в 18 веке - после того, как Ньютон и Лейбниц создали математический анализ.
21. Слово"Химия" вошло в научный обиход в 8 веке н.э. - когда арабы назвали так искусство египтян превращать одни вещества в другие. "Кемт" (варианты: "Кеми", "Кемет" - египтяне не отмечали на письме гласных звуков) - одно из древних имен Египта; но эллины называли эту страну иначе: "Айгюптос".
22. О существовании платины европейцы узнали только в 17 веке - после того, как ее обнаружили в Южной Америке и отличили от серебра по весу.
23. Платина - благородный металл: она не образует соединений, так что нет "платиновой руды", а есть самородки и песок. Точка плавления платины столь высока, что лишь электрическая дуга позволяет ее расплавить.
24. Получать из вина спирт или очень крепкую ("горючую") водку путем перегонки химики научились только в Средневековье.
25. Изготовлять из тел моллюсков пурпурну (но не "алую") краску умели финикийцы, а не египтяне. Греки не смогли узнать этот секрет, и он был забыт.
26. Никто из ученых Эллады и Античного мира не пытался связать ремесло химиков с выделением природных "стихий" в чистом виде. Объединение химии с философией ("алхимия") произошло лишь в Средневековье - в Исламском мире.
27. Ни Пифагор, ни Евклид не интересовались поисками "апейрона" - стихии, которую угадал Анаксимандр, но которая не связана с понятиями математики.
28. Архимед не увлекался химией; он занимался только теми науками, которые удается постичь, используя математику.
29. Рассуждения о "порче" металлов с помощью "кислот" и о существовании "универсального окислителя" начались в Средневековье - среди арабских ученых.
30. Догадку о том, что Солнце - раскаленный камень, высказал Анаксагор задолго до Архимеда. Но он считал, что метеориты - осколки Солнца, так что оно состоит не из золота.
31. Гипотеза о происхождении планет от Солнца появилась только в 18 веке - в трудах Канта и Лапласа.
32. Гипотеза о наличии "основных" металлов в составе любого вещества появилась в Средние века среди арабских алхимиков. Но они считали основным металлом ртуть, а не золото.
33. Гипотезу об атомах, имеющих определенную форму, высказал Демокрит - современник Платона. Платон не принял эту гипотезу и всю жизнь боролся против нее.
34. Консул Аттилий Регул командовал римской армией и флотом во время первой Пунической войны: тогда Сиракузы мирно признали власть Рима, чтобы спастись от власти Карфагена.
35. Аттилий Регул был разбит и убит карфагенянами в Африке. Жители Сиракуз не были причастны к этому.
36. Во время второй Пунической войны Сиракузами правил царь Гиерон, а не Дионисий.
37. Ганнибал получал подкрепления не из Африки, а из Испании. Сицилия интересовала римлян, как источник зерна и как путь их будущего наступления на Карфаген.
38. Римской армией при Каннах командовал не Сципион, а консулы Эмилий Павел и Варрон.
39. После победы при Каннах Ганнибал не стал осаждать Рим: у него нехватало войск для такой задачи.
40. Царь Филипп 5, который правил в Македонии во время 2 Пунической войны и враждовал с Римом, был потомком не Александра Македонского, а одного из его полководцев - Антигона. Все дети Александра были убиты диадохами во время борьбы за наследие Александра.
41. Эпирский царь Пирр жил до начала Пунических войн.
42. Римский полководец Серторий жил в 1 веке до н.э. - после окончания Пунических войн.
43. Римской армией, осадившей Сиракузы, командовал консул Метелл. Он не имел поручения: привезти в Рим живого Архимеда. Римский сенат не интересовался учеными.
44. Евклид никогда не бывал в Риме, поскольку римляне той эпохи (и более поздних времен) не увлекались математикой.
45. Архимед был случайно убит во время штурма Сиракуз и не попал в плен к римлянам. Если бы он уцелел - его, вероятно, провели бы в числе прочих пленных во время триумфа в Риме, а потом продали бы в рабство.
46. Рим никогда не стал "ученейшим городом" Италии или Средиземноморья. Римляне относились к греческой учености, как к развлечению бездельников. Римского поэта Лукреция, написавшего научно-популярную поэму "О природе вещей", в Риме считали сумасшедшим.
47. Александрия попала под власть Рима через 180 лет после падения Сиракуз - при Октавиане Августе.
48. Греческий историк Полибий, написавший первую историю Рима и его войн, жил через полвека после падения Сиракуз и был свидетелем разрушения Карфагена римлянами. Полибий не был родственником Эратосфена.
49. Римская империя, созданная Августом, процветала около 250 лет - до начала гражданских войн между "солдатскими" императорами.

В заключение перечислим авторов самых удачных или самых интересных работ по истории на нынешнем турнире им. Ломоносова:

• Петр Мансилья-Круз (школа 57, 11 класс)
• Аникеева Татьяна (школа 57, 11 класс)
  (единственная девушка среди лауреатов)
• Георгий Рыбаков (гимназия 1510, 10 класс)
• Максим Корольков (школа 57, 9 класс)
• Илья Чирков (школа 1201, 8 класс)
  (лучший результат по тексту "Архимед")
• Андрей Волыхов (школа 444, 8 класс)
  (самая чёткая работа в младших классах)
• Дима Косов (гимназия 1543, 7 класс)

Конкурс по математике

Задачи

7-9 класс и младше

1. (7-9){a₁,a₂,...,a₂₀} - набор целых положительных чисел.
   Строим новый набор чисел {b₀,b₁,b₂,...} по следующему правилу:
   b₀ - количество чисел исходного набора, которые больше 0,
   b₁ - количество чисел исходного набора, которые больше 1,
   b₂ - количество чисел исходного набора, которые больше 2,
   и т.д., пока  не  пойдут  нули.  Докажите,  что сумма всех чисел исходного набора равна сумме всех  чисел нового набора.
   
   
2. (7-9)В треугольнике ABC точки A', B' и C' лежат на сторонах BC, CA и AB соответственно. Известно, что
   угол AC'B' = угол B'A'C,
   угол CB'A' = угол A'C'B,
   угол BA'C' = угол C'B'A.
   Докажите, что точки A', B', C'- середины сторон треугольника.
   
   
3. (7-9)Куб со стороной 10 разбит на 1000 кубиков с ребром 1. В каждом кубике записано число, при этом сумма чисел в каждом столбике из 10 кубиков (в любом из трёх направлений) равна 0. В одном из кубиков (обозначим его через A ) записана единица. Через кубик A проходит три слоя, параллельных граням куба (толщина каждого слоя равна 1). Найдите сумму всех чисел в кубиках, не лежащих в этих слоях.

Старшие классы (10-11)

1. (10-11){a₁,a₂,...,a₂₀} - набор целых положительных чисел.
   Строим новый набор чисел {b₀,b₁,b₂,...} по следующему правилу:
   b₀ - количество чисел исходного набора, которые больше 0,
   b₁ - количество чисел исходного набора, которые больше 1,
   b₂ - количество чисел исходного набора, которые больше 2,
   и т.д., пока  не  пойдут  нули.  Докажите,  что сумма всех чисел исходного набора равна сумме всех  чисел нового набора.
   
   
2. (10-11)Восемь бумажных кругов радиуса 1 уложены на плоскость таким образом, что их границы проходят через одну точку, причем эта точка находится внутри всей области плоскости, покрытой кругами. Эта область представляет собой многоугольник с криволинейными сторонами. Найдите его периметр.
   
   
3. (10-11)Некоторая группа психологов разработала тест, пройдя который каждый человек получает оценку - число Q - показатель его умственных способностей (чем больше Q, тем больше способности). Предположим, что каждый житель двух стран - А и Б получил своё Q. За рейтинг страны принимается среднее арифметическое значений Q всех жителей этой страны.
   а). Группа граждан страны А эмигрировала в страну Б. Возможно ли, что у обеих стран выросли их рейтинги?
   б). После этого группа граждан страны Б (в числе которых могут быть и бывшие эмигранты из А) эмигрировала в страну А. Возможно ли, что рейтинги обеих стран опять возросли?

Решения задач конкурса по математике

7-9 класс и младше

1. Смотрите решение задачи 1 для 10-11 классов.
2. Углы /AC'A' и /AB'A' равны, так как дополняют до 180^o равные углы /CB'A' и /A'C'B.
   Углы /B'AC' и /B'A'C' равны, так как дополняют до 180^o равные суммы /C'B'A+/AC'B' и /BA'C'+/B'A'C. Значит, AB'A'C' - параллелограмм, следовательно, AC'=B'A'.
   Аналогично доказывается, что BA'B'C' - параллелограмм, и C'B=B'A'. Отсюда следует, что AC'=C'B, т.е. C' - середина AB.
   Для точек B' и A' доказательство аналогично.
3. Куб состоит из 100 столбиков, поэтому сумма всех чисел равна нулю. Любой слой состоит из 10 столбиков, поэтому сумма чисел в нем также равна нулю.
   Чтобы получить искомую сумму, следует из суммы чисел во всем кубе вычесть суммы чисел в трех слоях, проходящих через данный кубик, затем прибавить суммы чисел в трех проходящих через него столбиках, являющихся попарными пересечениями этих слоев (поскольку мы их вычли дважды - с каждым из двух слоев), и, наконец, вычесть число, стоящее в данном кубике (так как мы его учли изначально, затем трижды вычли и трижды прибавили).
   Итого имеем: 0 - 3*0 + 3*0 - 1 = -1.

10-11 класы

1. Рассмотрим следующую конструкцию. Возьмем набор кубиков и будем строить из них "башенки" - столбики высотой a₁, a₂, ..., a_n (смотрите рисунок). Посчитаем двумя способами, сколько кубиков нам для этого понадобится. Считая по столбцам получаем, что количество кубиков равно сумме чисел первого набора. Другой способ подсчета - по слоям. Количество кубиков в первом слое (стоящих на полу) равно b₀=n, в следующем слое - b₁, и т. д., количество кубиков в i-м слое равно b_i.
   Поэтому общее число кубиков равно сумме чисел второго набора.
   Значит, суммы чисел обоих наборов совпадают.
   
   
   
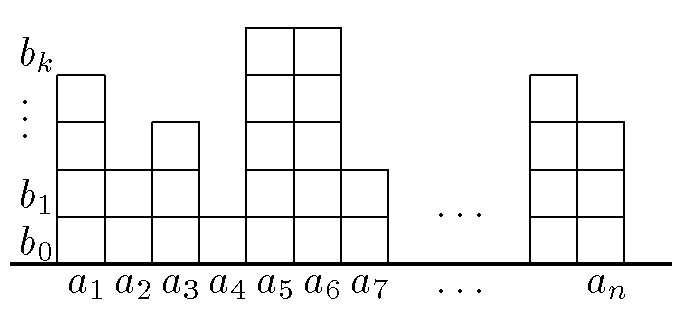
2. Обозначим точку пересечения окружностей через O. Проведем отрезки из точки O в вершины получившегося криволинейного многоугольника. Стороны многоугольника представляют собой дуги окружностей; по теореме о вписанном угле, величина каждой дуги равна удвоенному углу между отрезками, проведенными из точки O в ее концы. В сумме все эти углы составляют 360^o, поэтому сумма величин всех дуг равна 720^o, т.е. двум полным окружностям. Значит, сумма длин дуг равна 4p; это и есть искомый периметр.
   
   
3. Докажем сначала следующее интуитивно очевидное утверждение.

   Лемма. Если объединить две группы людей с рейтингами R₁ и R₂ (R₁ < R₂), то рейтинг R получившейся группы будет удовлетворять условию R₁ < R < R₂.

   Действительно, если Q'₁, Q'₂, ..., Q_n - показатели людей из первой группы, а Q''₁, Q''₂, ..., Q''_m - показатели людей из второй группы, то
   (n+m)R=Q'₁+...+Q'_n+Q''₁+...+ Q''_m=nR₁+mR₂

   Так как R₁ < R₂, то R=(n/(n+m))R₁+(m/(n+m))R₂ < (n/(n+m))R₂+(m/(n+m))R₂=R₂, и аналогично R > R₁, причем равенство в обоих случаях достигается тогда и только тогда, когда R₁=R₂.
   Лемма доказана.

   Из леммы следует, что если рейтинг страны выше (соответственно, равен или ниже) рейтинга группы эмигрантов, то после эмиграции он повышается (соответственно, остается прежним или понижается). Действительно, достаточно применить лемму к двум группам: эмигрантов и остающихся в стране.

   Аналогично, если рейтинг страны ниже (соответственно, равен или выше) рейтинга группы иммигрантов, то после иммиграции он повышается (соответственно, остается прежним или понижается), но по прежнему остается ниже (соответственно, равен или выше) рейтинга группы иммигрантов.

   Пример для пункта а) теперь строится просто. Достаточно, чтобы из А в Б эмигрировал всего один человек, имеющий показатель Q ниже, чем рейтинг страны А, но выше, чем рейтинг страны Б. Итак, в пункте а) ответ положительный.

   Такая ситуация возможна только если рейтинг страны А выше рейтинга страны Б, причем это же остается справедливым и после миграции. Но тогда невозможно, чтобы после обратной миграции из Б в А рейтинги обеих стран снова повысились. Поэтому, ответ в пункте б) отрицательный.

Конкурс по математическим играм

Инструкция проводящему математические игры

Математические игры проводятся для школьников 7 - 9 (и меньше) классов. Основная цель - заинтересовать школьников математикой, пригласить на математические кружки.

Спортивная сторона - на втором месте.

За 5 часов, отведенных на Турнир, Вы должны провести несколько (3 - 4) сеансов математических игр (каждый сеанс по часу - полтора). После заполнения Вашей аудитории прекращайте пускать новых детей и вешайте на дверь объявление о начале следующего сеанса.

Каждый сеанс проходит так. Сначала Вы предлагаете школьникам одну из игр. Нужно, чтобы они поиграли в нее между собой, с Вами. Цель состоит в том, чтобы объяснить школьникам, что такое выигрышная стратегия; на примерах показать, как можно доказывать, что один из игроков всегда сможет выиграть при любой игре другого. При этом Вы можете подсказывать школьникам, играть в поддавки. Если школьник уверенно предлагает четкую, но неверную стратегию, Вы можете поспорить с ним, что проиграете ему, пользуясь его (якобы выигрышной) стратегией (и осуществить это). В общем, игры - это творческий процесс.

Затем (сыграв со школьниками в одну - две игры) выдайте им задачу для самостоятельного решения. Они должны поиграть в эту игру друг с другом, или сами с собой, а затем каждый должен самостоятельно написать на листке бумаги, кто из игроков имеет выигрышную стратегию, какую, и почему эта стратегия выигрышная.

Собрав у школьников листки, отпустите их и готовьтесь к следующему сеансу.

В качестве результата Вы должны предоставить в оргкомитет список фамилий лучших школьников (с указанием имени, класса, школы и номера карточки) и указать выставленную оценку. Оценки бывают двух типов: "v" - ставится школьникам, успешно справившимся с задачей. Такие школьники получат диплом за победу в математических играх. "e" - ставится школьникам, неплохо показавшим себя, но недостаточно хорошо, чтобы считаться победителем матигр. Такие школьники, получив еще одну оценку "e" по какому-нибудь другому предмету, будут награждены дипломами за победу в многоборье.

Вы можете оценивать не только письменные решения, но и работу школьника во время сеанса.

Ниже приводятся варианты некоторых игр (в основном, на идею симметричной стратегии и передачи хода).

Вовсе не обязательно ограничиваться приведенным выше списком. Вы можете предлагать свои игры (на делимость, метод выигрышных позиций и т.д. и т.п.), важно лишь, чтобы задачи не были слишком сложны. Среди игр, выдаваемых для письменного решения старайтесь избегать игр, хорошо известных школьникам (а в качестве примеров годятся и всем известные игры). Впрочем, это не очень важно.

Условия математических игр

1. Двое по очереди ставят королей в клетки доски 9x9 так, чтобы они не били друг друга. Проигрывает тот, кто не может сделать ход. Кто выигрывает при правильной игре? А если доска 8x8?
2. На концах клетчатой полоски 1*n стоит по шашке. За ход разрешается сдвинуть любую шашку в направлении другой на одну или на две клетки. Перепрыгивать через шашку нельзя. Проигрывает тот, кто не может сделать ход. Кто выигрывает при правильной игре? Рассмотрите случаи разных n.
3. В начале есть одна кучка из n спичек. Разрешается за ход разбить любую кучку на две непустые. Кто не может сделать ход - проигрывает. Кто выигрывает при правильной игре сторон? Рассмотрите случаи разных n.
4. На каждой клетке доски m*n стоит по шашке. Игрок за один ход может снять с доски любое натуральное число шашек, стоящих подряд на вертикали или горизонтали. Кто не может сделать хода - проигрывает. Как закончится игра для различных m и n при наилучшей игре сторон?
5. Двое по очереди разламывают прямоугольную шоколадку. За один ход разрешается сделать прямолинейный разлом по любому из имеющихся углублений. Выигрывает тот, кто первым отломит дольку 1*1. Кто выигрывает при правильной игре?
   Рассмотрите случаи: небольшие значения m и n, размеры 10*4, 10*5, 5*1997, другие случаи.
6. Двое по очереди разламывают шоколадку. За один ход разрешается сделать прямолинейный разлом любого из имеющихся кусков вдоль углубления. Проигрывает тот, кто первым отломит дольку 1*1. Кто выигрывает при правильной игре, если шоколадка имеет размеры 10*10? Рассмотрите другие случаи.
7. На нескольких деревьях растут бананы. Играют двое. За ход разрешается съесть любое количество бананов с одного из деревьев. Проигрывает тот, кому нечего есть. Кто из играющих: начинающий, или его партнёр, может обеспечить себе победу, если имеется
   а) два дерева с одинаковым числом бананов;
   б)два дерева с разным числом бананов;
   в)три дерева c 1, 2 и 3 бананами соответственно;
   г)три дерева с одинаковым числом бананов;
   д)три дерева, на двух из которых одинаковое число бананов;
   е)Кто выигрывает, если на одном дереве 2 банана, а на остальных по 1?
   ж)Кто выигрывает, если на одном дереве 4 банана, а на остальных по 1 или 2?
   з)три дерева c 3, 5 и 7 бананами соответственно.
   Рассмотрите другие случаи.
8. На шахматной доске размером 8*8 расставлены ладьи: на каждом поле нижней линии - по белой ладье первого игрока, а на каждом поле верхней линии - по черной ладье второго игрока. Ходят по очереди, каждым ходом игрок может передвинуть одну из своих ладей по вертикали на любое число клеток навстречу вражеской ладье (перескакивать через чужую ладью нельзя). Проигрывает тот, кто не может сделать ход. Рассмотрите случаи других (прямоугольных) досок.

Решения математических игр

1. В случае 9*9 выигрывает первый: ставит короля в центральную клетку и далее ходит симметрично второму относительно центра.
2. В случаях вида n=3k+2 выигрывает второй, иначе - первый. Это легко проверить для n=3, 4, 5. Далее рассуждаем так: если полоска длины n=3k или n=3k+1, то первый может своим ходом перейти к доске размером 3k-1 и выиграть там по стратегии второго; если же полоска длины n=3k+2, то при любом ходе первого второй может своим ходом перейти к доске размером 3k-1 и выиграть.
3. Если спичек четное число, выигрывает первый: делит их на две одинаковые кучи и далее ходит симметрично первому.
   Если спичек нечетное число, то выигрывает второй. Одно из решений: после хода первого образуются куча с четным числом спичек и куча с нечетным числом спичек. Второй делит кучу с четным числом спичек на две равные и далее в этих двух кучах ходит симметрично первому. В результате игра сводится к игре с меньшим количеством нечетных спичек, и опять ход первого игрока.
4. Если одно из m и n нечетно, выигрывает первый: он снимает центральный ряд и далее ходит симметрично второму. Если и m и n четны, выигрывает второй: ходит симметрично центра доски.
5. Если одно из m и n четно, выигрывает первый: делит шоколадку на две одинаковые части и далее либо отламывает дольку 1*1, либо, если это невозможно, ходит симметрично последнему ходу второго.
   Если и m и n нечетны, игра более интересна (и сложна). Рассматривайте только конкретные ситуации.
6. Если одно из m и n четно (кроме случая 2*1), выигрывает первый: делит шоколадку на две одинаковые части и далее ходит симметрично ходам второго.
   Если и m и n нечетны, игра более интересна (и сложна). Рассматривайте только конкретные ситуации.
7. Эта и следующая игры - одна и та же игра "Ним". Стратегия в общем случае связана с двоичным разложением чисел и слишком сложна для начинающих школьников. Поэтому стоит задавать только конкретные ситуации.
   а)Выигрывает второй (симм. страт.).
   б)Выигрывает первый (сводит к п. а).
   в)Выигрывает второй (своим первым ходом он всегда может свести ситуацию к п. а)).
   г)Выигрывает первый (съедает целое дерево).
   д)Выигрывает первый (съедает третье дерево).
   е)Выигрывает первый.
   ж,з)Разберитесь сами.
8. Задача аналогична предыдущей --- рассматривается случай 8 деревьев с 6 бананами на каждом. Поиграйте на разных досках.

Задачи конкурса по лингвистике

1. (М.Е.Алексеев, А.Н.Журинский). Были взяты грузинские названия месяцев в их очередности с января по декабрь. Некоторые названия пропущены, но порядок следования остальных сохранен:
   bfydfhb, st,thdfkb, vfhnb, fghbkb, vfbcb, bdybcb, bdkbcb, jmnjv,thb, yjtv,thb\
   
   Переведите на русский язык грузинские названия месяцев и укажите их примерное произношение.
   Указание. Следует иметь в виду, что грузинские названия могут быть лишь частично сходны с соответствующими русскими, как, например, английские названия месяцев.
   
   
   
2. (Я.Г.Тестелец). Даны словосочетания на русском языке и их переводы на шведский:
   
   

   1.		ствол березы	-	stammen pЕ bjЖrken
   2.		футляр от очков	-	etuiet till glasЖgonen
   3.		звук взрыва	-	ljudet frЕn explosionen
   4.		страница газеты	-	sidan i tidningen
   5.		голова собаки	-	huvudet pЕ hunden
   6.		якорь корабля	-	ankaret till skeppet
   7.		дым от сигареты	-	rЖken frЕn cigaretten
   8.		член правительства	-	medlemmen i regeringen
   9.		батарейка приемника	-	batteriet till transistorn
   10.		спинка кресла	-	ryggstЖdet pЕ lДnstolen
   11.		шнурок ботинка	-	snЖren till skon
   12.		запах цветка	-	doften frЕn blomman
   13.		боец батальона	-	soldaten i bataljonen

   
   
   Заполните пропуски в следующих словосочетаниях, объяснив свое решение:
   

   а)		свет от лампы	-	skenet ... lampan
   б)		крыша здания	-	taket ... byggnaden
   в)		крышка кастрюли	-	locket ... kastrullen
   г)		статья закона	-	paragrafen ... lagen
   д)		участник заговора	-	deltagaren ... sammansvДrjningen

   
   Примечание. Е, Д, Ж - особые гласные шведского языка.
   
   
   
3. (И.Н.Шахова) Даны числительные языка хауса:
   лari bakwai da hamsin da shidda - 756
   sitta da лari bakwai da biyar - 6705
   saba'a da лari biyar da sittin - 7560
   
   А.Переведите с хауса: saba'in da biyar, лari shidda da sittin da shidda.
   Б.Запишите на хауса: 67; 5605.
   
   Примечание: ', л - особые согласные языка хауса.
   

   (Хауса - один из западно-чадских языков. На нем говорит от 30 до 40 млн. человек в Нигерии и ряде других стран Африки.)

Решения и ответы к задачам конкурса по лингвистике

1. Среди русских названий месяцев одинаковое начало имеют март и май, а также июнь и июль; последние два, кроме того, одинаковы по длине. Это справедливо и для грузинских названий. (Отыскать их помогает и то, что май - второй месяц после марта, а июнь и июль следуют подряд.) Первая пара дает нам буквы, которые предположительно соответствуют русским м, а, р и др., вторая пара - н и л. Подставляя эти буквы в опознанные названия месяцев, узнаем некоторые другие буквы и в результате получаем следующее чтение (прочерк поставлен на место букв, которые остаются неопознанными):

   иануари, -эбэруали, марти, а-рили, маи-и, иуни-и, иули-и, о-томбэри, ноэмбэри.

   (Чтение буквы, которая здесь записана как и, остается не вполне ясным, так как она может соответствовать также русскому й или ий.)

   • Звуковое значение некоторых букв отличается от ожидаемого. Так, первый звук в слове 'февраль' - [т] придыхательное, предпоследний звук в словах 'май', 'июнь' и 'июль' - [с].

2. Анализируя условие, определяем значения сочетаний шведских предлогов с существительными:
   
   pЕ - 'неотъемлемая часть',
   till - 'дополнительная часть, приложение',
   frЕn - 'то, что исходит от чего-л.',
   i - 'однородная часть'.
   

   Ответы:
   skenet frЕn lampan,
   taket pЕ byggnaden,
   locket till kastrullen,
   paragrafen i lagen,
   deltagaren i sammansvДrjningen.

3. 
   A. 75, 666.
   Б. sittin da bakwai, hamsa da лari shidda da biyar.

Задачи и задания конкурса по физике

После номера задачи в скобках указано, каким классам эта задача рекомендуется. Решать задачи не своего класса разрешается. Обращайте внимание на качество физических объяснений: работа, в которой хорошо, с объяснениями, решены две-три задачи, будет высоко оценена - выше, чем работа, в которой имеются нечёткие рассуждения по многим задачам.

1. (7-11, экспериментальная) Имеется прибор, в состав которого входят две лампочки, два патрона и два выключателя. Одним выключателем можно включать и выключать одну лампочку, другим --- другую, независимо от того, в какой из патронов вкручена каждая лампочка. Предложите способ изготовления такого прибора.
   Примечание: такой прибор имеется у члена жюри, проводящего конкурс. Вы можете или "разгадать" схему именно этого устройства, или предложить свою.
2. (10-11, экспериментальная) У жюри имеется прибор с тремя контактами (A, B и C) и вольтметр. Результаты измерений этим вольтметром напряжений между точками A и B, B и C, C и A таковы, что их числовые значения не могут являться сторонами треугольника. Укажите причину, по которой это может происходить.
3. (7-9) Петя вымыл стакан горячей водой и поставил его на стол вверх дном. Через некоторое время стакан вдруг сам собой передвинулся. Помогите Пете разобраться, как такое может быть.
4. (9-11) Человек наблюдает за вертикальным падением камня. В момент времени t₁ высота камня была h₁=100 м. Через 2 секунды (в момент времени t₂) высота стала h₂=10 м.
   С какой высоты падал камень?
5. (7-8) Недавно в Москве был сильный ураган, поваливший и вырвавший с корнем много деревьев. Трава, которую, казалось бы, выдрать намного проще, чем дерево, при этом практически не пострадала. Почему?
6. (9-11) Рассказывают, что один скептически настроенный физик, наблюдая по телевизору прямую трансляцию высадки первого человека на Луну, внимательно посмотрел на Нейла Армстронга, на его приборчик, который висел на поясе у Нейла на шнуре, на свои часы и через некоторое время сказал: "Действительно, это не постановка, а Луна!". Почему он так решил?
7. (10-11) В колбу, заполненную водой, вставлена пробка с капилляром (см. рисунок). Между пробкой и поверхностью воды находится небольшое количество воздуха. Колбу поставили на газовую плиту и начали греть. Качественно постройте график зависимости высоты жидкости в капилляре от времени.
   
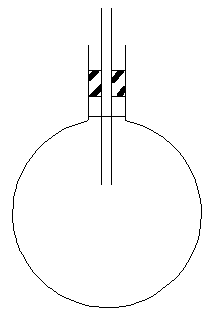
8. (10-11) На гладкой горизонтальной поверхности на одной из боковой граней лежит призма. Углы призмы, прилежащие к этой грани, равны соответственно a и b. Сверху на призму равномерно вертикально падают со скоростью v маленькие шарики. Ударившись об грань призмы, они упруго отскакивают, больше не взаимодействуя ни с призмой, ни с другими шариками. Найти установившуюся скорость призмы.
   
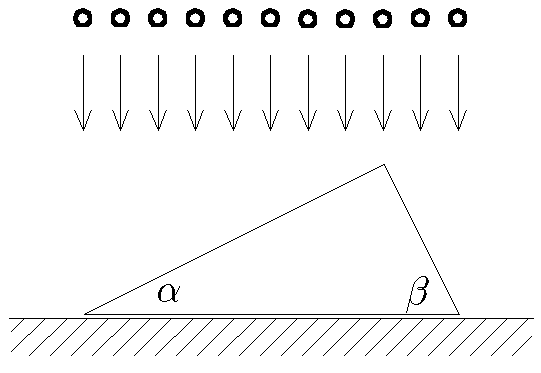
9. (9-11) На весах стоит свечка. Как изменятся показания весов, если свечку зажечь?
10. (7-9) В эксперименте по проверке закона Кулона необходимо было следить за показаниями прибора, расположенного внутри сферы, причём делать в сфере дырки или деформировать её нельзя (должна быть целая сферическая проводящая поверхность). Но если сферу сделать целиком из металла, то расположенный внутри измерительный прибор не будет виден и невозможно будет наблюдать его показания. Учёным удалось найти очень простой способ решения этой проблемы. Какой?
11. (7-10) Распечатали бутылку с газированной водой. Качественно изобразите график зависимости температуры газированной воды от времени с момента вскрытия упаковки.

Закрытие Турнира и награждение успешно выступивших состоится в воскресенье 15 ноября 1998 года в 10 часов в Московском Авиационном институте

Проезд до станции метро "Сокол". Выход из метро в центре зала по коридору в ту сторону, где на указателе есть троллейбусы 12 и 70, но нет трамваев (на правую сторону Ленинградского проспекта, если смотреть в направлении от центра города на высотное здание института "Гидропроект"). Троллейбусная остановка находится напротив выхода из метро. Проехать на троллейбусе 12-го или 70-го маршрута до остановки "Авиационный и Пищевой институты". Далее пройти по ходу движения троллейбуса, из которого Вы вышли, вдоль Волоколамского шоссе (по которому Вы ехали), свернуть на первую улицу направо (Дубосековская улица), пройти по ней примерно 200 метров до большой площадки, вымощенной плиткой. Вход в институт через большой стеклянный вестибюль, расположенный с той стороны площадки, которая ближе к Волоколамскому шоссе.

Не нужно пытаться пройти через другие вестибюли, а также через проходную МАИ на Волоколамском шоссе --- там Вас не пропустят.