Рисунок 1.
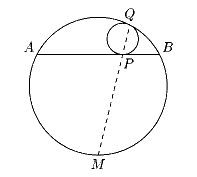
Задача 0.1 В окружности w проведена хорда AB, точка M - середина одной из дуг AB. В сегмент s окружности w , стягиваемый хордой AB и не содержащий точку M, вписана окружность w1, касающаяся хорды AB и окружности w в точках P и Q соответственно (рис.1). Докажите, что прямая PQ проходит через M.
Задача 0.2 Докажите, что в условиях задачи 0.1 точка M имеет одну и ту же степень относительно всевозможных окружностей w1, вписанных в сегмент s. Эта степень равна MA2.
Напомним, что степень точки относительно окружности - это произведение отрезков секущей от данной точки до двух точек пересечения с окружностью, взятое со знаком "+", если точка лежит вне окружности, и со знаком "-", если внутри. Как известно, указанное произведение не зависит от выбора секущей. Далее, множество точек плоскости, имеющих одинаковые степени относительно двух различных окружностей есть прямая, перпендикулярная линии центров этих окружностей (докажите). Эта прямая называется радикальной осью двух данных окружностей. Если окружности пересекаются, то радикальная ось проходит через точки пересечения окружностей. Предыдущая задача утверждает, таким образом, что радикальная ось любой пары окружностей, вписанных в сегмент s, проходит через M.
Задача 1.1 Треугольник ABC вписан в окружность w . A0, B0 - середины сторон BC и CA соответственно; A', B' - середины дуг BC и CA, не содержащих A и B соответственно. Построим на отрезках A0A' и B0B' как на диаметрах окружности wA и wB. Докажите, что общая касательная к окружностям wA, wB, "ближайшая" к AB, параллельна AB.
Задача 1.2 Задачу 1.1 можно обобщить следующим образом. Пусть треугольник ABC вписан в окружность w . A0, B0 - точки на сторонах BC и CA соответственно, такие что прямая A0B0 параллельна AB. В сегменты, стягиваемые хордами BC и CA окружности w, не содержащие A и B соответственно, вписаны окружности wA, wB, касающиеся хорд BC и CA в точках A0, B0. Докажите, что общая касательная к окружностям wA, wB, "ближайшая" к AB, параллельна AB (рис.2).
Задача 1.3 Пусть в обозначениях задачи 1.2 A', B' - точки касания окружностей w1, w2 с окружностью w, C' - середина дуги AB, не содержащей C. Обозначим KA, KB точки пересечения отрезков AC и B'C', CB и C'A' соответственно. Докажите, что прямая KAKB параллельна AB. Если точки A0, B0 - середины сторон BC и CA, то прямая KAKB проходит через центр вписанной окружности DABC.
Задача 2.1 Пусть треугольник ABC вписан в окружность w, точки A0, B0, C0 - середины его сторон, точки A', B', C' - середины дуг BC, CA, AB окружности w, не содержащих соответственно A, B, C. Построим на отрезках A0A', B0B' и C0C' как на диаметрах окружности wA, wB и wC. Для каждой пары из этих трех окружностей проведем общую внешнюю касательную, "ближайшую" к соответствующей стороне DABC. Обозначим эти касательные lA, lB, lC. Пусть прямая lA касается окружности wB в точке TAB. Аналогичным образом определим точки касания TBA, TBC, TCB, TCA, TAC. Докажите, что отрезки касательных TABTAC, TBCTBA и TCATCB равны (рис.3).
Задача 2.2 В обозначениях задачи 2.1 докажите, что точки TAB, TBA, TBC, TCB, TCA, TAC лежат на одной окружности. Какая точка является центром этой окружности?
Задача 2.3 В обозначениях задачи 2.1 пусть A''B''C'' - треугольник, получающийся в пересечении прямых lA, lB, lC (A'' - точка пересечения lB и lC, и т. д.). Докажите, что TACC''= TBCC''=A''B''=AB/4.
Таким образом, отрезки касательных TABTAC, TBCTCB и TCATAC равны "покусочно", а DA''B''C'' всегда гомотетичен DABC с коэффициентом -1/4. Длина каждого из отрезков TABTAC, TBCTBA, TCATCB равна четверти периметра DABC.
Задача 2.4 В обозначениях задачи 2.1 пусть pA - прямая, проходящая через A' перпендикулярно линии центров окружностей wB, wC. Аналогично определим прямые pB, pC. Докажите, что прямые pA, pB, pC проходят соответственно через точки A'', B'', C'' и пересекаются в одной точке.
Задача 2.5 В окружность w вписан четырехугольник ABCD. В сегменты, стягиваемые хордами AB, BC, CD, DA вписываются окружности, касающиеся соответствующей хорды в ее середине. К парам окружностей, касающихся последовательных сторон четырехугольника, проведены внешние касательные, "ближайшие" к диагоналям (рис 4). Докажите, что в пересечении этих касательных получается ромб тогда и только тогда, когда ABCD - равнобокая трапеция.
Приводим схему геометрического решения
Задачи 1.1-1.2 а) Пусть I0 - центр вписанной окружности треугольника A0B0C. Если TCA - ближайшая к прямой AB точка окружности wA, то середина дуги AB (точка C'), TCA и A' лежат на одной прямой (задача 0.1). Также TCA, A0 и I0 лежат на одной прямой.
б) Если A0, B0 - середины сторон DABC, то точки C', TCB, TCA, I0 лежат на одной окружности. Подсчет углов дает параллельность TCATCB и AB
в) Пусть A0, B0 таковы, что A0B0 параллельна AB. A0A' проходит через середину дуги BAC. Отсюда подсчетом углов получаем, что точки A0, A', I0, C лежат на одной окружности.
г) Треугольники C'I0TCA и C'A'I0 подобны, и значит C'TCA*C'A'= (C'I0)2 . Следовательно, C' имеет одну и ту же степень относительно окружностей wA, wB.
Задача 1.3 Применим теорему Дезарга к треугольникам I0A0B0 и C'KAKB. Если A0, B0 - середины сторон DABC, то KAKB проходит через центр вписанной окружности по теореме Паскаля (рис.5).
Задача 2.1 а) Точки B', TCB, TBC, C' лежат на одной прямой.
б) Из подсчета углов вытекает, что DA''TCBTBC равнобедренный: A''TCB=A''TBC.
Задача 2.2 Центр окружности совпадает с центром вписанной окружности DA''B''C''. Нетрудно показать, что он равноудален от всех точек касания.
Задача 2.3 Пусть OC - центр окружности wC. Тогда треугольники C''TACOC и AC0C' подобны с коэффициентом 1/2. Отсюда TACC''=TBCC''=AB/4. Аналогично TBAA''=TCAA''=BC/4 и TCBB''=TABB''=CA/4. Из задачи 2.1 следует, что A''B''=(1/4)AB+c, B''C''=(1/4)BC+c, C''A''=(1/4)CA+c, где c - некоторая константа. Но A''B'':AB=B''C'':BC=C''A'':CA из подобия, отсюда c=0 в случае неравностороннего DABC. Случай равностороннего DABC легко разобрать отдельно; также можно рассмотреть его как предел неравносторонних треугольников.
Задача 2.4 Прямые pA, pB, pC - радикальные оси пар окружностей из wA, wB, wC.
Задача 2.5 Из предыдущих задач следует, что указанный четырехугольник всегда параллелограмм. Если четырехугольник - ромб, то легко видеть (рис.4), что TABTAD+ TCBTCD- TBATBC- TDATDC=0 или (1/4)( pABD+ pCBD- pABC- pDBC )=0, откуда следует равенство диагоналей AC и BD.

Рисунок 1.
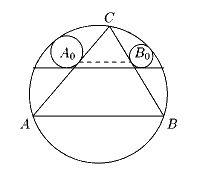
Рисунок 2.
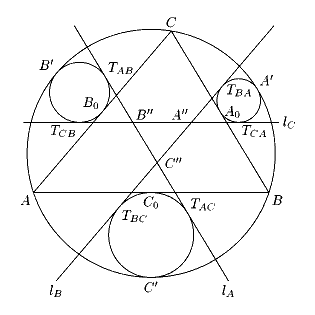
Рисунок 3.
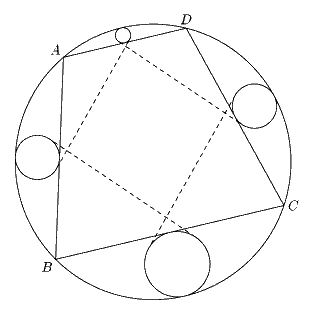
Рисунок 4.